题目内容
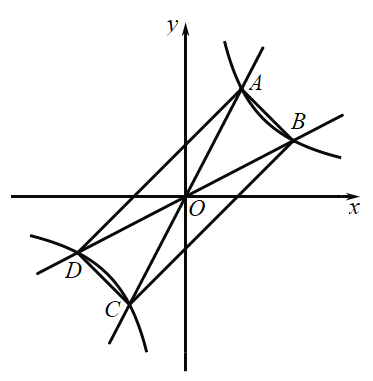
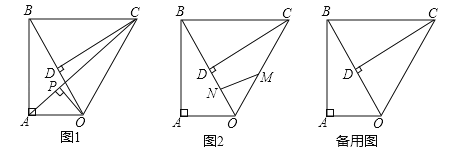
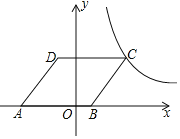
【题目】已知:△ABC和△ADE按如图所示方式放置,点D在△ABC内,连接BD、CD和CE,且∠DCE=90°.

(1)如图①,当△ABC和△ADE均为等边三角形时,试确定AD、BD、CD三条线段的关系,并说明理由;
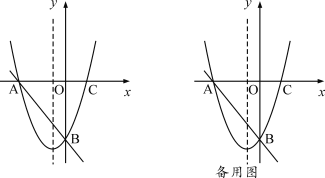
(2)如图②,当BA=BC=2AC,DA=DE=2AE时,试确定AD、BD、CD三条线段的关系,并说明理由;
(3)如图③,当AB:BC:AC=AD:DE:AE=m:n:p时,请直接写出AD、BD、CD三条线段的关系.
【答案】(1)CD2+BD2=AD2,理由见解析;(2)CD2+![]() BD2=AD2,理由见解析;(3)(mCD)2+(pBD)2=(nAD)2
BD2=AD2,理由见解析;(3)(mCD)2+(pBD)2=(nAD)2
【解析】
(1)先判断出∠BAD=∠CAE,进而判断出△ABD≌△ACE,最后用勾股定理即可得出结论;
(2)先判断出△ABC∽△ADE,进而得出∠BAC=∠DAE,即可判断出△BAD∽△CAE,最后用勾股定理即可得出结论;
(3)先判断出△ABC∽△ADE,进而得出∠BAC=∠DAE,即可判断出△BAD∽△CAE,最后用勾股定理即可得出结论.
解:(1)CD2+BD2=AD2,
理由:∵△ABC和△ADE是等边三角形,
∴AB=AC,AD=AE=DE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
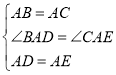 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
在Rt△DCE中,
CD2+CE2=DE2,
∴CD2+BD2=AD2,
(2)CD2+![]() BD2=AD2,
BD2=AD2,
理由:∵BA=BC=2AC,DA=DE=2AE,
∴![]() ,
,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,
∴∠BAD=∠CAE,
∵![]() ,
,
∴△BAD∽△CAE,
∴![]() =2,
=2,
∴BD=2CE,
在Rt△DCE中,CD2+CE2=DE2,
∴CD2+![]() BD2=AD2,
BD2=AD2,
(3)(mCD)2+(pBD)2=(nAD)2,
理由:∵AB:BC:AC=AD:DE:AE=m:n:p,
∴DE=![]() AD,△ABC∽△ADE,
AD,△ABC∽△ADE,
∴∠BAC=∠DAE,
∵![]() ,
,
∴△ABD∽△ACE,
∴![]() ,
,
∴CE=![]() BD,
BD,
在Rt△DCE中,CD2+CE2=DE2,
∴CD2+![]() BD2=
BD2=![]() AD2,
AD2,
∴(mCD)2+(pBD)2=(nAD)2

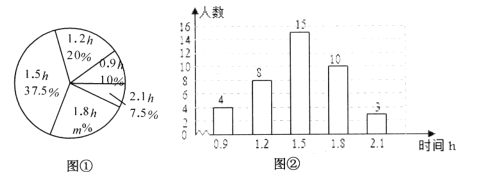
【题目】某校团委为了解该校七年级学生最喜欢的课余活动情况,采用随机抽样的方法进行了问卷调查,被调查学生必须从“运动、娱乐、阅读、其他”四项中选择其中的一项,以下是根据调查结果绘制的统计图表的一部分,

活动类型 | 频数(人数) | 频率 |
运动 | 20 | |
娱乐 | 40 | |
阅读 | ||
其他 | 0.1 |
根据以上图表信息,解答下列问题:
(1)在被调查的学生中,最喜欢“运动”的学生人数为 人,最喜欢“娱乐”的学生人数占被调查学生人数的百分比为 %.
(2)本次调查的样本容量是 ,最喜欢“其他”的学生人数为 人.
(3)若该校七年级共有360名学生,试估计最喜欢“阅读”的学生人数.