��Ŀ����
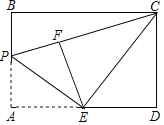
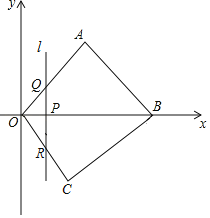
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���OABC�Ķ���O������ԭ�㣬��OAB��90����OA��AB��OB��8��OC��5��
��1�����A�����ꣻ
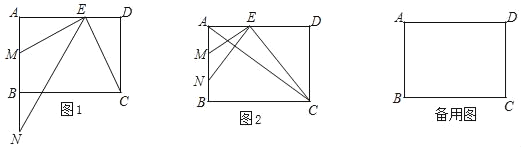
��2����P�Ǵ�O���������X�������᷽����ÿ��1��λ���ȵ��ٶ��˶�����B��һ�����㣨��P�����O��B�غϣ�������P��ֱ��l��y��ƽ�У����ı���ABCD�ı�AO��AB�ڵ�Q����OC��BC�ڵ�R�����˶�ʱ��Ϊt��s������֪t��3ʱ��ֱ��lǡ�þ����� C��
��ٵ�P����ʱͬʱ��EҲ�ӵ�B��������ÿ��1����λ���ٶ����O�˶�����Pֹͣʱ��EҲֹͣ������QRE�����ΪS����0��t��3ʱS��t�ĺ�����ϵʽ����ֱ��д��S�����ֵ��
���Ƿ����ijһʱ��t��ʹ����OREΪֱ�������Σ������ڣ��������Ӧt��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��A��4��4������2����![]() ��S�����ֵΪ
��S�����ֵΪ![]() ����t��ֵΪ4��
����t��ֵΪ4��![]() .
.
��������
��1�����ݵ���ֱ�������ε����ʼ��ɽ�����⣻
��2�����������ֱ��OA��OB��OC��BC�Ľ���ʽ�������P��Q�����꼴�ɽ�����⣻���ɱ�ʾ��QR��PE�ij������ɵõ��������������ʽ�����䷽�������ֵ���ɣ�
�ڷ�����������ۣ�����REO��90�����ORE��90�����ROE��90���ֱ���⼴�ɣ�
�⣺��1����������OAB�ǵ���ֱ�������Σ�
��OB��8����B��8��0��
��A��4��4����
��2����A��4��4����B��8��0����
��ֱ��OA�Ľ���ʽΪy��x��ֱ��AB�Ľ���ʽy����x+6��
��t��3ʱ��ֱ��lǡ�ù���C����OP��3��OC��5��
��PR��4��C��3����4����
��ֱ��OC�Ľ���ʽΪy��-![]() x��ֱ��BC�Ľ���ʽΪy��
x��ֱ��BC�Ľ���ʽΪy��![]() ��
��
�ٵ�0��t��3ʱ��Q��t��t����R��t��-![]() t����
t����
��QR=t-(-![]() t)=
t)=![]() ��PE��8��2t��
��PE��8��2t��
��S��![]() ��
��
��t��2ʱ��S�����ֵΪ![]() ��
��
��Ҫʹ��OREΪֱ�������Σ��������������
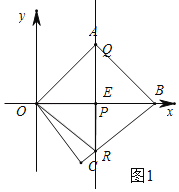
��������REO��90������ͼ1�����P��E���غϣ�
��8��2t��0�����t��4��
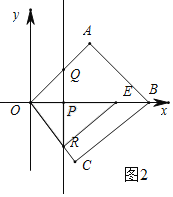
��������ORE��90������ͼ2����ORP�ס�REP��
��![]() ����RP2��OPPE��
����RP2��OPPE��
��![]() ��
��
��֮�ã�t��![]() ��
��
��
��ʹ����OREΪֱ��������ʱ��t��ֵΪ��4��![]() ��
��

 ��Ԫ������ĩ��ϵ�д�
��Ԫ������ĩ��ϵ�д�