题目内容
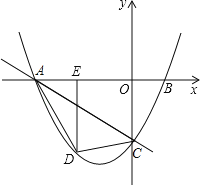
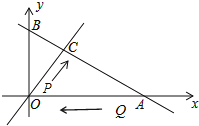
【题目】如图,直线m:y=kx(k>0)与直线n:![]() 相交于点C,点A、B为直线n与坐标轴的交点,∠COA=60°,点P从O点出发沿线段OC向点C匀速运动,速度为每秒1个单位,同时点Q从点A出发沿线段AO向点O匀速运动,速度为每秒2个单位,设运动时间为t秒.
相交于点C,点A、B为直线n与坐标轴的交点,∠COA=60°,点P从O点出发沿线段OC向点C匀速运动,速度为每秒1个单位,同时点Q从点A出发沿线段AO向点O匀速运动,速度为每秒2个单位,设运动时间为t秒.
(1)k= ;
(2)记△POQ的面积为S,求t为何值时S取得最大值;
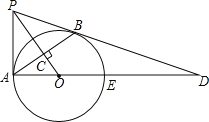
(3)当△POQ的面积最大时,以PQ为直径的圆与直线n有怎样的位置关系,请说明理由.
【答案】(1)k=![]() ;(2)当t=
;(2)当t=![]() 时,S有最大值;(3)直线AB与以PQ为直径的圆O相离,理由详见解析.
时,S有最大值;(3)直线AB与以PQ为直径的圆O相离,理由详见解析.
【解析】
(1)依据k=tan∠COA进行求解即可;
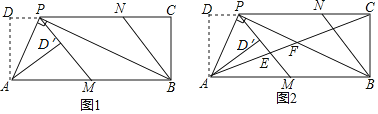
(2)如图1所示:过点P作PD⊥OA,垂足为D.由锐角三角函数的定义和特殊锐角三角函数值可求得PD=![]() ,然后利用三角形的面积公式列出关系式,最后利用配方法求得三角形面积最大时t的值即可;
,然后利用三角形的面积公式列出关系式,最后利用配方法求得三角形面积最大时t的值即可;
(3)如图2所示:过点P作PD⊥OA垂足为D,过圆心O作OE⊥AB,垂足为E.首先证明四边形,四边形OPCE为矩形,然后求得d和r的值即可.
(1)k=tan∠COA=tan60°=![]() .
.
(2)如图1所示:过点P作PD⊥OA,垂足为D.

令直线n:y=﹣![]() x+2
x+2![]() 的y=0得:﹣
的y=0得:﹣![]() x+2
x+2![]() =0,解得x=6,
=0,解得x=6,
∴OA=6.
∵∠COA=60°,PD⊥OA,
∴![]() ,即
,即![]() .
.
∴PD=![]() .
.
![]()
∴当t=![]() 时,S有最大值.
时,S有最大值.
(3)如图2所示:过点P作PD⊥OA垂足为D,过圆心O作OE⊥AB,垂足为E.

令直线n:y=﹣![]() x+2
x+2![]() 的x=0得:y=2
的x=0得:y=2![]() .
.
∴OB=2![]() .
.
∵tan∠BAO=![]() ,
,
∴∠BAO=30°.
∴∠ABO=60°.
∴OC=OBsin60°=2![]() =3.
=3.
∵∠COA=60°,
∴∠BOC=30°.
∴∠BOC+∠OBC=90°.
∴∠OCA=90°.
当t=![]() 时,OD=
时,OD=![]() =
=![]() ,PD=
,PD=![]() .DQ=3﹣
.DQ=3﹣![]() =
=![]() .
.
∴tan∠PQO= .
.
∴∠PQO=30°.
∴∠BAO=∠PQO.
∴PQ∥AB,
∴∠CPQ+∠PCA=180°.
∴∠CPQ=180°﹣90°=90°.
∴∠ECP=∠CPO=∠OEC=90°.
∴四边形OPCE为矩形.
∴d=OE=PC=OC﹣OP=3﹣![]() =
=![]() .
.
PQ=OQsin60°=3×![]() .
.
∴r=PO=![]() .
.
∵d>r.
∴直线AB与以PQ为直径的圆O相离.