题目内容
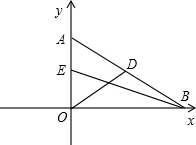
在△ABC中,BC=a,AC=b,AB=c,∠C=90°,CD和BE是△ABC的两条中线,且CD⊥BE,那么a:b:c=( )
| A.1:2:3 | B.3:2:1 | C.
| D.1:
|
可以用建立直角坐标系来做.以三角形BC所在的边为x轴,以AC所在的边为y轴,C点为原点建立直角坐标系.
可得,C(0,0),B(a,0),A(0,b).
∵CD和BE为中线,
∴D,E为中点,则D(
,
),E(0,
).
则直线BE的斜率是:
=-
;
直线CD的斜率是:
=
.
∵CD与BE垂直,所以CD与BE所在直线的斜率的乘积为-1,即-
•
=-1.
∴b2=2a2.
∴a:b=1:
.
又∵a2+b2=c2.
∴a:b:c=1:
:
.
故选D.
可得,C(0,0),B(a,0),A(0,b).
∵CD和BE为中线,
∴D,E为中点,则D(
| a |
| 2 |
| b |
| 2 |
| b |
| 2 |
则直线BE的斜率是:
-
| ||
| a |
| b |
| 2a |
直线CD的斜率是:
| ||
|
| b |
| a |
∵CD与BE垂直,所以CD与BE所在直线的斜率的乘积为-1,即-
| b |
| 2a |
| b |
| a |
∴b2=2a2.
∴a:b=1:
| 2 |
又∵a2+b2=c2.
∴a:b:c=1:
| 2 |
| 3 |
故选D.


练习册系列答案
相关题目






