题目内容
如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD．
（1）求证：△BCE≌△DCF；
（2）若AB=15，AD=7，BC=5，求CE的长．
（1）求证：△BCE≌△DCF；
（2）若AB=15，AD=7，BC=5，求CE的长．
（1）证明：∵AC平分∠BAD，CE⊥AB于E，CF⊥AD于F
∴CE=CF，
在Rt△BCE和Rt△DCF中，
∵CE=CF，BC=CD，
∴Rt△BCE≌Rt△DCF （HL）．（3分）
（2）∵Rt△BCE≌Rt△DCF，
∴DF=EB，CE=CF，CE⊥AB于E，CF⊥AD于F，
∴Rt△ACE≌Rt△ACF，
∴AF=AE，（2分）
∵AB=15，AD=7，
∴AD+DF=AB-EB，
∴EB=DF=4，（2分）
在Rt△BCE中，根据勾股定理，CE=3．（1分）
∴CE=CF，
在Rt△BCE和Rt△DCF中，
∵CE=CF，BC=CD，
∴Rt△BCE≌Rt△DCF （HL）．（3分）
（2）∵Rt△BCE≌Rt△DCF，
∴DF=EB，CE=CF，CE⊥AB于E，CF⊥AD于F，
∴Rt△ACE≌Rt△ACF，
∴AF=AE，（2分）
∵AB=15，AD=7，
∴AD+DF=AB-EB，
∴EB=DF=4，（2分）
在Rt△BCE中，根据勾股定理，CE=3．（1分）
练习册系列答案
相关题目
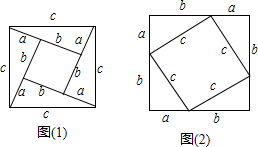数学中一个十分著名的定理，这个定理结论的数学表达式是______．
