题目内容
【题目】如图1,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,过点D作AC的平行线交AB于点O,DE⊥AD交AB于点E.
(1)求证:点O是AE的中点;
(2)若点F是AC边上一点,且OF=OA,连接EF,如图2,判断EF与AC的位置关系,并说明理由;
(3)在(2)的条件下,试探究线段AE、AF、AC之间满足的等量关系,并说明理由
【答案】(1)见解析;(2)EF⊥AC,理由见解析;(3)AE+AF=2AC,理由见解析.
【解析】
(1)根据直角三角形、角平分线和平行线的性质证明∠ODA=∠OAD,∠OED=∠ODE,进而得出OD=OA,OD=OE即可解决问题;
(2)结论:EF⊥AC.先证明OF=OE=OA,再根据等腰三角形的性质以及三角形内角和是180°即可解决问题;
(3)结论:AE+AF=2AC.延长ED交AC的延长线于M.证明AE=AM,CM=CF即可解决问题.
证明:如图1中,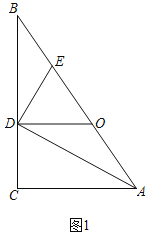
∵AD平分∠BAC,
∴∠CAD=∠BAD,
∵OD∥AC,
∴∠ODA=∠DAC,
∴∠ODA=∠OAD,
∴OD=OA,
∵DE⊥AD,
∴∠ADE=90°,
∴∠EDO+∠ADO=90°,∠DEO+∠OAD=90°,
∴∠OED=∠ODE,
∴OD=OE,
∴OE=OA,
∴点O是AE的中点;
(2)解:结论:EF⊥AC.
理由:如图2中,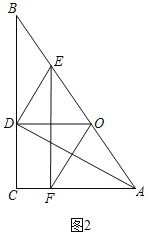
∵OF=OA,OA=OE,
∴OF=OE,∠OFA=∠OAF,
∴∠OEF=∠OFE,
∵∠OEF+∠OFE+∠OFA+∠OAF=180°,
∴∠OFE+∠OFA=90°,即∠EFA=90°,
∴EF⊥AC;
(3)解:如图3中,结论:AE+AF=2AC.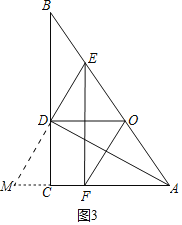
理由:延长ED交AC的延长线于M.
∵AD⊥EM,
∴∠ADM=∠ADE=90°,
∴∠M+∠DAM=90°,∠AED+∠DAE=90°,
∵∠DAM=∠DAE,
∴∠M=∠AED,
∴AE=AM,
∴DM=DE,
∵∠DCA=∠EFA=90°,
∴DC∥EF,
∵DM=DE,
∴CM=CF,
∵AE-AF=AM-AF=FM=2CF,AC-AF=CF,
∴AE-AF=2(AC-AF),
∴AE+AF=2AC.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案