题目内容
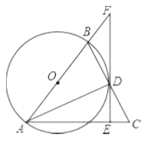
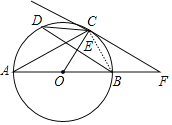
【题目】如图,AB为⊙O的直径,CD为⊙O的弦,连接AC,BD,半径CO交BD于点E,过点C作切线,交AB的延长线于点F,且∠CFA=∠DCA.

(1)求证:OE⊥BD;
(2)若BE=4,CE=2,则⊙O的半径是 ,弦AC的长是 .
【答案】(1)见解析;(2)5,4![]()
【解析】
(1)根据圆周角定理得到∠ABD=∠DCA,则∠CFA=∠ABD,则可判断BD∥CF,接着根据切线的性质得OC⊥CF,然后根据平行线的性质得到结论;
(2)连接BC,设⊙O的半径为r,在Rt△OBE中利用勾股定理得到(r﹣2)2+42=r2,求出r得到⊙O的半径为5,再利用勾股定理计算出BC=2![]() ,接着利用圆周角定理得到∠ACB=90°,然后利用勾股定理计算AC.
,接着利用圆周角定理得到∠ACB=90°,然后利用勾股定理计算AC.
(1)证明:∵∠CFA=∠DCA,∠ABD=∠DCA,
∴∠CFA=∠ABD,
∴BD∥CF,
∵CF为⊙O的切线,
∴OC⊥CF,
∴OC⊥BD,即OE⊥BD;
(2)解:如图,连接BC,
设⊙O的半径为r,则OE=r﹣2,OB=r,
在Rt△OBE中,(r﹣2)2+42=r2,
解得r=5,即⊙O的半径为5,
在Rt△BCE中,BC=![]() ,
,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC=![]() .
.
故答案为5,![]() .
.

练习册系列答案
相关题目
【题目】某礼品店从文化用品市场批发甲、乙、丙三种礼品(每种礼品都有),各礼品的数量和批发单价列表如下:
甲 | 乙 | 丙 | |
数量(个) |
|
|
|
批发单价(元) |
|
|
|
|
![]() 当
当![]() 时,若这三种礼品共批发
时,若这三种礼品共批发![]() 个,甲礼品的总价不低于丙礼品的总价,求
个,甲礼品的总价不低于丙礼品的总价,求![]() 的最小值.
的最小值.
![]() 已知该店用
已知该店用![]() 元批发了这三种礼品,且
元批发了这三种礼品,且![]() .
.
![]() 当
当![]() 时,若批发这三种礼品的平均单价为
时,若批发这三种礼品的平均单价为![]() 元/个,求
元/个,求![]() 的值.
的值.
![]() 当
当![]() 时,若该店批发了
时,若该店批发了![]() 个丙礼品,且
个丙礼品,且![]() 为正整数,求
为正整数,求![]() 的值.
的值.