题目内容
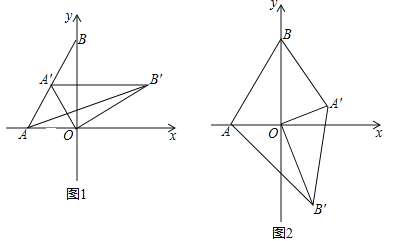
【题目】如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0,![]() ).
).
(1)求∠BAO的度数;
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1,△BA′O的面积为S2,S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
【答案】(1) ∠BAO=60°;(2) S1=S2;(3) S1=S2不发生变化;理由见解析.
【解析】
试题分析:(1)先求出OA,OB,再利用锐角三角函数即可得出结论;
(2)根据等边三角形的性质可得AO=AA',再根据直角三角形30°角所对的直角边等斜边的一半求出AO=![]() AB,然后求出AO=AA’,,然后再根据等边三角形的性质求出点O到AB的距离等于点A'到AO的距离,然后根据等底等高的三角形的面积相等解答;
AB,然后求出AO=AA’,,然后再根据等边三角形的性质求出点O到AB的距离等于点A'到AO的距离,然后根据等底等高的三角形的面积相等解答;
(3)根据旋转的性质可得BO=OB',AA'=OA',再求出∠AON=∠A'OM,然后再证明ΔAON≌ΔA'OM,可得AN=A'M,然后利用等底等高的三角形面积相等证明.
试题解析:(1)∵A(﹣1,0),B(0,![]() ),
),
∴OA=1,OB=![]() ,
,
在Rt△AOB中,tan∠BAO=![]() =
=![]() ,
,
∴∠BAO=60°;
(2)∵∠BAO=60°,∠AOB=90°,
∴∠ABO=30°,
∴CA'=AC=![]() AB,
AB,
∴OA'=AA'=AO,
根据等边三角形的性质可得,△AOA'的边AO、AA'上的高相等,
∴△BA'O的面积和△AB'O的面积相等(等底等高的三角形的面积相等),
即S1=S2.
(3)S1=S2不发生变化;
理由:如图,过点'作A'M⊥OB.过点A作AN⊥OB'交B'O的延长线于N,
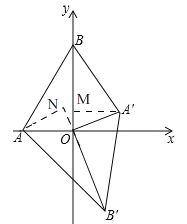
∵△A'B'O是由△ABO绕点O旋转得到,
∴BO=OB',AO=OA',
∵∠AON+∠BON=90°,∠A'OM+∠BON=180°﹣90°=90°,
∴∠AON=∠A'OM,
在△AON和△A'OM中,
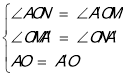 ,
,
∴△AON≌△A'OM(AAS),
∴AN=A'M,
∴△BOA'的面积和△AB'O的面积相等(等底等高的三角形的面积相等),
即S1=S2.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案【题目】用![]() 纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.
纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.
设在同一家复印店一次复印文件的页数为![]() (
(![]() 为非负整数).
为非负整数).
(1)根据题意,填写下表:
一次复印页数(页) | 5 | 10 | 20 | 30 | … |
甲复印店收费(元) |
| 2 | … | ||
乙复印店收费(元) |
|
| … |
(2)设在甲复印店复印收费![]() 元,在乙复印店复印收费
元,在乙复印店复印收费![]() 元,分别写出
元,分别写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)当![]() 时,顾客在哪家复印店复印花费少?请说明理由.
时,顾客在哪家复印店复印花费少?请说明理由.