题目内容
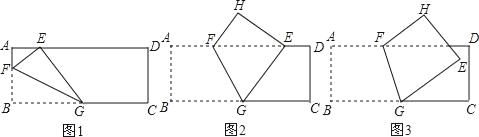
【题目】问题情境:在综合与实践课上,同学们以“已知三角形三边的长度,求三角形面积”为主题开展数学活动,小颖想到借助正方形网格解决问题.图1,图2都是8×8的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.

操作发现:小颖在图1中画出△ABC,其顶点A,B,C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE,EF分别经过点C,A,她借助此图求出了△ABC的面积.
(1)在图1中,小颖所画的△ABC的三边长分别是AB=__________,BC=__________,AC=__________;△ABC的面积为__________.
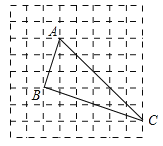
解决问题:(2)已知△ABC中,AB=![]() ,BC=2
,BC=2![]() ,AC=5
,AC=5![]() ,请你根据小颖的思路,在图2的正方形网格中画出△ABC,并计算△ABC的面积.
,请你根据小颖的思路,在图2的正方形网格中画出△ABC,并计算△ABC的面积.
【答案】(1)5;![]() ;
;![]() ;
;![]() ;(2)见解析,△ABC的面积:10.
;(2)见解析,△ABC的面积:10.
【解析】
(1)根据方格与勾股定理即可求出各边长,再利用大正方形的面积减去各边上的直角三角形面积即可求出△ABC的面积;(2)根据三角形的边长,利用勾股定理的逆定理知其为直角三角形,故利用方格可画出图形,再利用割补法即可求出面积.
(1)AB=![]() =5,BC=
=5,BC=![]() =
=![]() ,
,
AC=![]() =
=![]() ,
,
△ABC的面积为:4×4–![]() ×3×4–
×3×4–![]() ×1×4–
×1×4–![]() ×3×1=
×3×1=![]() ,
,
故答案为:5;![]() ;
;![]() ;
;![]() ;
;
(2)补图如下.△ABC的面积:6×5–![]() ×3×1–
×3×1–![]() ×5×5–
×5×5–![]() ×2×6=10.
×2×6=10.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目