题目内容
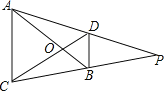
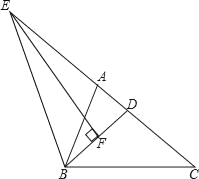
【题目】在△ABC中,BD平分∠ABC,EF垂直平分BD交CA延长线于点E.
(1)求证:ED2=EAEC;
(2)若ED=6,BD=CD=3,求BC的长.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)根据EF是BD的垂直平分线,可得EB=ED,再证明△EAB∽△EBC,列比例式为![]() ,将EB与ED替换可得结论;
,将EB与ED替换可得结论;
(2)根据△EAB∽△EBC,得![]() ,代入可得EA=4,作高线AG、DH,根据勾股定理求EF=
,代入可得EA=4,作高线AG、DH,根据勾股定理求EF=![]() ,利用面积法可得DH的长,再用平行相似得:△AGE∽△DHE,列比例式得AG的长,从而得EG的长,根据勾股定理得BC的长.
,利用面积法可得DH的长,再用平行相似得:△AGE∽△DHE,列比例式得AG的长,从而得EG的长,根据勾股定理得BC的长.
详解:(1)证明:∵EF是BD的垂直平分线,
∴EB=ED,
∴∠EDB=∠EBD,
∵∠EDB=∠C+∠DBC,∠EBD=∠ABE+∠ABD,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠C=∠ABE,
∵∠BEC=∠BEA,
∴△EAB∽△EBC,
∴![]() ,
,
∴EB2=EAEC,
∵EB=ED,
∴ED2=EAEC;
(2)∵ED=EB=6,BD=CD=3,
∴EC=6+3=9,
由(1)知:△EAB∽△EBC,
∴![]() ,
,
∴![]() ,EA=4,
,EA=4,
过A作AG⊥EB于G,过D作DH⊥EB于H,
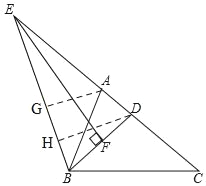
Rt△EFD中,ED=6,DF=![]() ,
,
∴EF=![]() ,
,
∴S△EBD=![]() EBDH=
EBDH=![]() BDEF,
BDEF,
∴DH=![]() EF=
EF=![]() ,
,
∵AG∥DH,
∴△AGE∽△DHE,
∴![]() ,
,
∴![]() ,
,![]() ,
,
由勾股定理得:EG=![]() ,
,
∴BG=6﹣![]() =
=![]() ,
,
由勾股定理得:AB=![]() ,
,
∵△EAB∽△EBC,
∴![]() ,
,
∴![]() ,
,
∴BC=![]() .
.

练习册系列答案
相关题目