题目内容
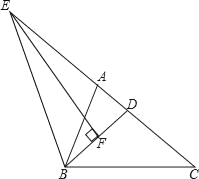
【题目】如图，已知△ABC为等边三角形，点D、E分别在边BC、AC上，且AE=CD，AD与BE相交于点F．则∠BFD的度数为（ ）
A. 45° B. 90° C. 60° D. 30°
【答案】C
【解析】根据等边三角形性质得出AB=AC，∠BAE=∠C=60°，证△ABE≌△CAD，推出∠ABE=∠CAD，根据三角形外角性质求出∠BFD=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC，即可求出答案．
∵△ABC是等边三角形，
∴AB=AC，∠BAE=∠C=60°，
在△ABE和△CAD中，
∵AB=AC，
∠BAE=∠C，
AE=CD，
∴△ABE≌△CAD(SAS)，
∴∠ABE=∠CAD，
∴∠BFD=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC=60
故选：C.
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
