题目内容
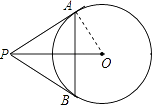
【题目】已知:如图,⊙O的半径是5cm,PA、PB切⊙O于点A、B两点,∠PAB=60°.求AB的长. 
【答案】解:连接AO,
∵PA、PB分别与相切⊙O于点A、B,
∴PA=PB,∠APO= ![]() ∠APB,
∠APB,
∵∠PAB=60°,
∴△ABP是等边三角形,
∴∠APO=30°,
∵∠PAO=90°,
∴PO=10,PA=5 ![]() ,
,
∴PA=AB=5 ![]() .
.
【解析】首先连接OA,由PA、PB分别与相切⊙O于点A、B,∠PAB=60°,易得△ABP是等边三角形,则可求得AP的长,继而求得答案.
【考点精析】本题主要考查了切线的性质定理的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.

练习册系列答案
相关题目