题目内容
【题目】阅读下列材料:
1637 年笛卡儿(R.Descartes,1596 1650)在其《几何学》中,首次应用待定系数法将 4 次方程分解为两个 2 次方程求解,并最早给出因式分解定理.
他认为,若一个高于二次的关于 x 的多项式能被 (![]() ) 整除,则其一定可以分解为 (
) 整除,则其一定可以分解为 (![]() ) 与另外一个整式的乘积,而且令这个多项式的值为 0 时, x = a 是关于 x 的这个方程的一个根.
) 与另外一个整式的乘积,而且令这个多项式的值为 0 时, x = a 是关于 x 的这个方程的一个根.
例如:多项式![]() 可以分解为 (
可以分解为 (![]() ) 与另外一个整式 M 的乘积,即
) 与另外一个整式 M 的乘积,即 ![]()
令![]() 时,可知 x =1 为该方程的一个根.
时,可知 x =1 为该方程的一个根.
关于笛卡尔的“待定系数法”原理,举例说明如下: 分解因式:![]()
观察知,显然 x=1 时,原式 = 0 ,因此原式可分解为 (![]() ) 与另一个整式的积.
) 与另一个整式的积.
令:![]() ,则
,则![]() =
=![]() ,因等式两边 x 同次幂的系数相等,则有:
,因等式两边 x 同次幂的系数相等,则有: ,得
,得![]() ,从而
,从而![]()
此时,不难发现 x= 1 是方程 ![]() 的一个根.
的一个根.
根据以上材料,理解并运用材料提供的方法,解答以下问题:
(1)若![]() 是多项式
是多项式![]() 的因式,求 a 的值并将多项式
的因式,求 a 的值并将多项式![]() 分解因式;
分解因式;
(2)若多项式![]() 含有因式
含有因式![]() 及
及![]() ,求a+ b 的值.
,求a+ b 的值.
【答案】(1)![]() ;(2)a+ b=
;(2)a+ b=![]()
【解析】
(1)已知多项式的因式,将多项式分解为该因式与另外一个整式乘积的形式,将这个新构造的式子中的系数与原式中的系数进行对照,列方程即可得到答案
(2)已知多项式中含有因式,根据材料中的内容可知因式的解为零,所以解得未知数的值,再利用未知数的值带入原式即可求解到参数的值,将结果相加即可求得答案
(1)令:![]() ,
,
因等式两边 x 同次幂的系数相等,则有: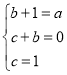 ,
,
解得: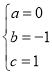 ,
,
从而![]() =x3+1=(x+1)(x2-x+1);
=x3+1=(x+1)(x2-x+1);
(2)设![]() (其中M为二次整式),
(其中M为二次整式),
由材料可知:x+1=0或x-2=0;
所以:x=-1,x=2是方程![]() 的解,
的解,
所以![]() ,
,
解得a=8,b=-39,
∴a+b=8+(-39) =-31.

 考前必练系列答案
考前必练系列答案