Question

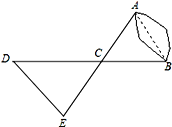
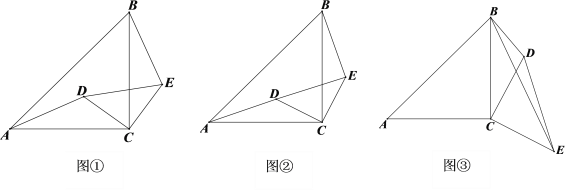
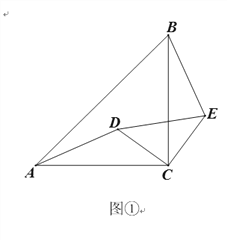
【题目】如图①已知△ACB和△DCE为等腰直角三角形，按如图的位置摆放，直角顶点

C重合．

（1）求证：AD=BE；

（2）将△DCE绕点C旋转得到图②，点A、D、E在同一直线上时，若CD=,BE=3，

求AB 的长；

（3）将△DCE绕点C顺时针旋转得到图③，若∠CBD=45°，AC=6，BD=3，求BE的长．

Answer 1

【答案】（1）证明见解析；（2）；（3）9

【解析】（1）利用等腰直角三角形的性质求出∠ACD=∠ECB，用SAS证明△ACD≌△BCE即可；（2）利用（1）的结论∠AEB=90°，在Rt△AEB中，用勾股定理求出AB；（3）连接AD, 求出∠ABD=90°，在Rt△ADB中，用勾股定理求出AD，由△ACD≌△BCE即可求得BE．

解：（1）∵△ACB和△DCE为等腰直角三角形

∴AC=CB，DC=CE，

∠ACB=90°, ∠DCE=90°

∴∠ACB-∠DCB =∠DCE-∠DCB

即∠ACD=∠ECB

∴△ACD≌△BCE (SAS)

∴AD=BE

（2）解：

∵△DCE为等腰直角三角形

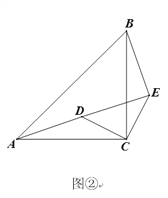
∴DC=EC=

∴DE=2

∵△ACD≌△BCE (SAS)

∴AD=BE=3

∠ADC=∠BEC=180°-45°=135°

∴∠AEB=135°-45°=90°

在Rt △AEB中，AB=

（3）连接AD,

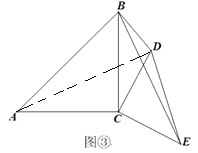
∵△ACB为等腰直角三角形

∴AC=BC=6, ∠ABC=45°

∴AB=

∵∠CBD=45°

∴∠ABD=45°+45°=90°

在Rt △ADB中，AD=

∵△ACD≌△BCE (SAS)

∴AD=BE=9

“点睛”本题考查了等腰直角三角形的性质、全等三角形及勾股定理的运用，解题关键是证明两个三角形全等，解题时要考虑辅助线的作法．