题目内容
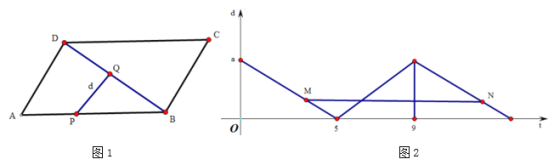
【题目】动点P在□ABCD边上沿着![]() 的方向匀速移动,到达点
的方向匀速移动,到达点![]() 时停止移动.已知P的速度为
时停止移动.已知P的速度为![]() 个单位长度/
个单位长度/![]() ,其所在位置用点
,其所在位置用点![]() 表示,
表示,![]() 到对角线
到对角线![]() 的距离(即垂线段
的距离(即垂线段![]() 的长)为
的长)为![]() 个单位长度,其中
个单位长度,其中![]() 与
与![]() 的函数图像如图②所示.
的函数图像如图②所示.
(1)若a=3,求当t=8时△BPQ的面积;
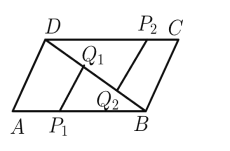
(2)如图②,点M,N分别在函数第一和第三段图像上,线段![]() 平行于横轴,
平行于横轴,![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() 、
、![]() .设
.设![]() 、
、![]() 时点P走过的路程分别为
时点P走过的路程分别为![]() 、
、![]() ,若
,若![]() +
+![]() =16,求
=16,求![]() 、
、![]() 的值.
的值.
【答案】(1)![]() ;(2)3.5;12.5
;(2)3.5;12.5
【解析】
(1)由题意知:当a=3时,点P在A点,此时PQ最长为a,即此时PQ=3,当P点运动到点B时,此点P和点B重合,即PQ为0,则此时P点运动路程为AB的长度,由图象可知AB=5,当点P继续运动到点C时,此时PQ最长即PQ=3,可推出AB=CD=5,AD=BC=4,可得当t=8时,P点在BC边上,即AB+BP=8,则BP=3,即对应的时间是t=5和t=9之间的函数图象,求出这一段的函数解析式,再把t=8代入,求出对应的d,即可求出BQ,则可求出△BPQ的面积;
(2)由题意可得l1=t1,l2=t2,即t1+t2=16①,再根据M,N平行于x轴,可推出AP1=CP2,即t1=t2-9②,联立①,②即可求出![]() 、
、![]() 的值.
的值.
(1)如图:

由题意知:当a=3时,点P在A点,此时PQ最长为a,即此时PQ=3,
当P点运动到点B时,此点P和点B重合,即PQ为0,
则此时P点运动路程为AB的长度,由图象可知AB=5,
当点P继续运动到点C时,此时PQ最长即PQ=3,(用全等三角形可易证,
此BC的长度为:BC=9-5=4,
即AB=CD=5,AD=BC=4,
∴当t=8时,P点在BC边上,即AB+BP=8,则BP=3,
则对应的时间是t=5和t=9之间的函数图象,
设此时函数为d=kt+b,把(5,0),(9,3)代入函数则有![]() ,
,
解得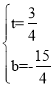 ,
,
∴d=![]() t
t![]() ,
,
把t=8代入,则d=![]() ×8
×8![]() =
=![]() ,
,
在△BPQ中,BQ=![]() =
=![]() ,
,
∴S△BPQ=![]() BQ·PQ=
BQ·PQ=![]() ×
×![]() ×
×![]() =
=![]() ;
;
(2)由题意可得l1=t1,l2=t2,
∵l1+l2=16,
∴t1+t2=16①,
∵MN平行于x轴,
∴yM=yN,
即此时d的值相同,
∴AP1=CP2,
即t1=t2-9②,
联立①,②得: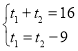 ,
,
解得: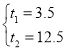 ,
,
∴t1=3.5,t2=12.5.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案