题目内容
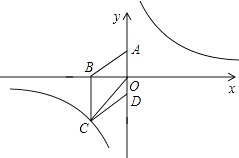
【题目】如图，在△ABC中，已知AB=AC=5，BC=6，且△ABC≌△DEF，将△DEF与△ABC重合在一起，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE、始终经过点A，EF与AC交于M点． 
（1）求证：△ABE∽△ECM；
（2）探究：在△DEF运动过程中，重叠部分能否构成等腰三角形？若能，求出BE的长；若不能，请说明理由；
（3）当线段AM最短时，求重叠部分的面积．
【答案】
（1）证明：∵AB=AC，
∴∠B=∠C，
∵△ABC≌△DEF，
∴∠AEF=∠B，
又∵∠AEF+∠CEM=∠AEC=∠B+∠BAE，
∴∠CEM=∠BAE，
∴△ABE∽△ECM
（2）能．
解：∵∠AEF=∠B=∠C，且∠AME＞∠C，
∴∠AME＞∠AEF，
∴AE≠AM；
当AE=EM时，则△ABE≌△ECM，
∴CE=AB=5，
∴BE=BC﹣EC=6﹣5=1，
当AM=EM时，则∠MAE=∠MEA，
∴∠MAE+∠BAE=∠MEA+∠CEM，
即∠CAB=∠CEA，
又∵∠C=∠C，
∴△CAE∽△CBA，
∴ 
，
∴CE= 
，
∴BE=6﹣ 
= 
；
∴BE=1或
（3）解：设BE=x，
又∵△ABE∽△ECM，
∴ 
，
即： 
，
∴CM=﹣ 
+ 
x=﹣ 
（x﹣3）2+ 
，
∴AM=5﹣CM═ （x﹣3）2+ 
，
∴当x=3时，AM最短为 ，
又∵当BE=x=3= 
BC时，
∴点E为BC的中点，
∴AE⊥BC，
∴AE= 
=4，
此时，EF⊥AC，
∴EM= 
= 
，
S△AEM= 
．
【解析】（1）由AB=AC，根据等边对等角，可得∠B=∠C，又由△ABC≌△DEF与三角形外角的性质，易证得∠CEM=∠BAE，则可证得：△ABE∽△ECM；（2）首先由∠AEF=∠B=∠C，且∠AME＞∠C，可得AE≠AM，然后分别从AE=EM与AM=EM去分析，注意利用全等三角形与相似三角形的性质求解即可求得答案；（3）首先设BE=x，由△ABE∽△ECM，根据相似三角形的对应边成比例，易得CM=﹣ + x=﹣ （x﹣3）2+ ，继而求得AM的值，利用二次函数的性质，即可求得线段AM的最小值，继而求得重叠部分的面积．
【考点精析】关于本题考查的二次函数的最值和勾股定理的概念，需要了解如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案．
