题目内容
【题目】如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(﹣4,0).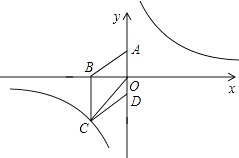
(1)求经过点C的反比例函数的解析式;
(2)设P是(1)中所求函数图象上一点,以P、O、A顶点的三角形的面积与△COD的面积相等.求点P的坐标.
【答案】
(1)
解:由题意知,OA=3,OB=4
在Rt△AOB中,AB= ![]()
∵四边形ABCD为菱形
∴AD=BC=AB=5,
∴C(﹣4,﹣5).
设经过点C的反比例函数的解析式为 ![]() (k≠0),
(k≠0),
则 ![]() =﹣5,解得k=20.
=﹣5,解得k=20.
故所求的反比例函数的解析式为 ![]()
(2)
解:设P(x,y)
∵AD=AB=5,OA=3,
∴OD=2,S△COD= ![]()
即 ![]() ,
,
∴|x|= ![]() ,
,
∴ ![]()
当x= ![]() 时,y=
时,y= ![]() =
= ![]() ,当x=﹣
,当x=﹣ ![]() 时,y=
时,y= ![]() =﹣
=﹣ ![]()
∴P( ![]() )或(
)或( ![]() )
)
【解析】(1)根据菱形的性质可得菱形的边长,进而可得点C的坐标,代入反比例函数解析式可得所求的解析式;(2)设出点P的坐标,易得△COD的面积,利用点P的横坐标表示出△PAO的面积,那么可得点P的横坐标,就求得了点P的坐标.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目