题目内容
 如图,以△ABC的边BC为直径作⊙O,分别交AB、AC于点D、E,过E作BC的垂线交BC于点F,交⊙O于M,P是弧BC中点,连接PC交EM于点G,若AB=13,AE=5,tan∠BGF=4.求:(1)EM的长;(2)AD的长.
如图,以△ABC的边BC为直径作⊙O,分别交AB、AC于点D、E,过E作BC的垂线交BC于点F,交⊙O于M,P是弧BC中点,连接PC交EM于点G,若AB=13,AE=5,tan∠BGF=4.求:(1)EM的长;(2)AD的长.
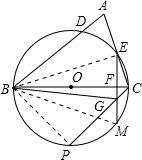 解:(1)连接BE、BP,BM,
解:(1)连接BE、BP,BM,则∠BEC=90°,∠P=90°,
∵P为弧BC中点,
∴∠BCP=∠CBP=45°,
∵EM⊥BC与F,
∴∠EFC=90°,
于是△CFG为等腰直角三角形,GF=FC,
又∵tan∠BGF=4,
设BF=4x,则FG=x,于是FC=x,
根据射影定理,BE2=BF•BC=4x•5x,
即122=20x2,x2=
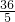 ,x=
,x=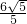 .
.根据相交弦定理,EF2=BF•CF,得EF2=4x•x,
EF2=4x2=4×
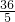 =
= ,EF=
,EF= ;
;EM=2×
 =
=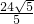 .
.(2)在Rt△BEC中,根据射影定理,EC2=BC•CF=5x•x=5×
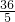 =36,解得EC=6或EC=-6(负值舍去).
=36,解得EC=6或EC=-6(负值舍去).根据割线定理AD•AB=AE•AC,
得13AD=5×(5+6),
解得AD=
 .
.分析:(1)连接BE、BP,构造直角三角形,利用射影定理求出BC、CF,BF、CE的长,进而求出EF的长,得到EM的长;
(2)利用割线定理AD•AB=AE•AC,可求得AD的长.
点评:此题综合考查了直角三角形的性质、相交弦定理、射影定理等知识,难度较大.解答此题的关键是作出辅助线,构造直角三角形,利用其性质解答.

练习册系列答案
相关题目
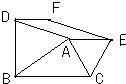 26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.
26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.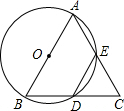 如图,以△ABC的边AB为直径作⊙O,交BC于D点,交AC于E点,BD=DE
如图,以△ABC的边AB为直径作⊙O,交BC于D点,交AC于E点,BD=DE
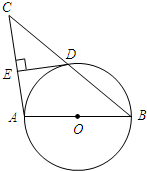 (2011•峨眉山市二模)如图,以△ABC的边AB为直径作⊙O,BC与⊙O交于D,D是BC的中点,过D作DE⊥AC,交AC于点E.
(2011•峨眉山市二模)如图,以△ABC的边AB为直径作⊙O,BC与⊙O交于D,D是BC的中点,过D作DE⊥AC,交AC于点E.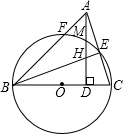 (2010•黔东南州)如图,以△ABC的边BC为直径作⊙O分别交AB,AC于点F.点E,AD⊥BC于D,AD交于⊙O于M,交BE于H.
(2010•黔东南州)如图,以△ABC的边BC为直径作⊙O分别交AB,AC于点F.点E,AD⊥BC于D,AD交于⊙O于M,交BE于H.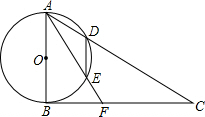 如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF
如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF