题目内容
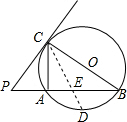
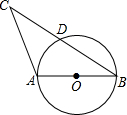
已知:如图,⊙O是△ABC的外接圆,且AB=AC=13,BC=24,PA是⊙O的切线,A为切点,割 线PBD过圆心,交⊙O于另一点D,连接CD.
线PBD过圆心,交⊙O于另一点D,连接CD.
(1)求证:PA∥BC;
(2)求⊙O的半径及CD的长.
 线PBD过圆心,交⊙O于另一点D,连接CD.
线PBD过圆心,交⊙O于另一点D,连接CD.(1)求证:PA∥BC;
(2)求⊙O的半径及CD的长.
(1)证明:∵PA是⊙O的切线,
∴∠PAB=∠2.
又∵AB=AC,
∴∠1=∠2,
∴∠PAB=∠1.
∴PA∥BC.
(2)连接OA交BC于点G,则OA⊥PA;
 由(1)可知,PA∥BC,
由(1)可知,PA∥BC,
∴OA⊥BC.
∴G为BC的中点,
∵BC=24,
∴BG=12.
又∵AB=13,
∴AG=5.
设⊙O的半径为R,则OG=OA-AG=R-5,
在Rt△BOG中,
∵OB2=BG2+OG2,
∴R2=122+(R-5)2,
∴R=16.9,OG=11.9;
∵BD是⊙O的直径,
∴DC⊥BC.
又∵OG⊥BC,
∴OG∥DC.
∵点O是BD的中点,
∴DC=2OG=23.8.
∴∠PAB=∠2.
又∵AB=AC,
∴∠1=∠2,
∴∠PAB=∠1.
∴PA∥BC.
(2)连接OA交BC于点G,则OA⊥PA;
 由(1)可知,PA∥BC,
由(1)可知,PA∥BC,∴OA⊥BC.
∴G为BC的中点,
∵BC=24,
∴BG=12.
又∵AB=13,
∴AG=5.
设⊙O的半径为R,则OG=OA-AG=R-5,
在Rt△BOG中,
∵OB2=BG2+OG2,
∴R2=122+(R-5)2,
∴R=16.9,OG=11.9;
∵BD是⊙O的直径,
∴DC⊥BC.
又∵OG⊥BC,
∴OG∥DC.
∵点O是BD的中点,
∴DC=2OG=23.8.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目