题目内容
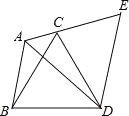
【题目】如图,已知△ABC,以BC为边向外作△BCD并连接AD,把△ABD绕着点D按顺时针方向旋转60°后得到△ECD,且点A,C,E在一条直线上,若AB=3,AC=2,求∠BAD的度数与AD的长?
【答案】60°;5.
【解析】
试题分析:根据旋转的性质得∠ADE=60°,DA=DE,∠BAD=∠E=60°,则可判断△ADE为等边三角形,所以∠E=60°,AD=AE,于是得到∠BAD=60°,再利用点A、C、E在一条直线上得到AE=AC+CE,再根据△ABD绕着点D按顺时针方向旋转60°后得到△ECD得到CE=AB,所以AE=AC+AB=5,进而得到AD的长.
试题解析:∵点A、C、E在一条直线上,而△ABD绕着点D按顺时针方向旋转60°后得到△ECD,
∴∠ADE=60°,DA=DE,∠BAD=∠E=60°,
∴△ADE为等边三角形,
∴∠E=60°,AD=AE,
∴∠BAD=60°,
∵点A、C、E在一条直线上,
∴AE=AC+CE,
∵△ABD绕着点D按顺时针方向旋转60°后得到△ECD,
∴CE=AB,
∴AE=AC+AB=2+3=5,
∴AD=AE=5.

练习册系列答案
相关题目