题目内容
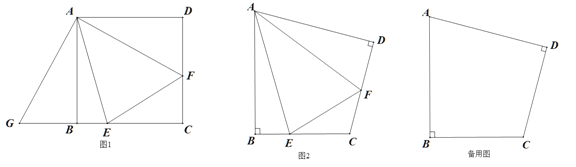
【题目】(1)如图1,在正方形ABCD中,E、F分别是边BC、CD上的点,且∠EAF=45°,把△ADF绕着点A顺时针旋转90°得到△ABG,请直接写出图中所有的全等三角形;
(2)在四边形ABCD中,AB=AD,∠B=∠D=90°.
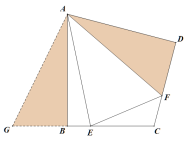
①如图2,若E、F分别是边BC、CD上的点,且2∠EAF=∠BAD,求证:EF=BE+DF;
②若E、F分别是边BC、CD延长线上的点,且2∠EAF=∠BAD,①中的结论是否仍然成立?请说明理由
【答案】(1)△ADF≌△ABG、△AEF≌△AEG;(2)①证明见解析;②不成立;理由见解析;
【解析】
(1)由旋转的性质易得△ADF≌△ABG、△AEF≌△AEG;
(2)①如图,将△ADF绕着点A顺时针旋转,使AD与AB重合,易证△ADF≌△ABG,故∠DAF=∠BAG,AF=AG,DF=BG,由2∠EAF=∠BAD得∠EAF=∠EAG,从而得△AEF≌△AEG,易得证;
②不成立.如图,将△ADF绕着点A顺时针旋转,使AD与AB重合,得△ABH,可证得△AEF≌△AEH,从而得出EF=BE-DF.
(1)△ADF≌△ABG、△AEF≌△AEG;
(2)①如图,将△ADF绕着点A顺时针旋转,使AD与AB重合,得△ABG,
∵AB=AD,∠ABC=∠D=![]() ,
,
∴∠ABC+∠ABG=![]() 即∠GBC=
即∠GBC=![]() ,
,
易得△ADF≌△ABG,
∴∠DAF=∠BAG,AF=AG,DF=BG,
∵2∠EAF=∠BAD,
∴∠EAF=∠BAE+∠DAF=∠BAE+∠BAG=∠EAG,
∵AE=AE,
∴△AEF≌△AEG,
∴EF=EG=BE+BG=BE+DF,
即EF=BE+DF.
②不成立
理由如下:如图,将△ADF绕着点A顺时针旋转,使AD与AB重合,得△ABH,
∵AB=AD,∠B=∠ADC=∠ADF=![]()
∴点H在BC上,易得AF=AH,BH=DF,∠1=∠2
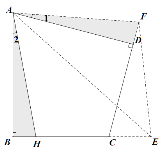
∴∠EAF=∠EAD+∠1=∠EAD+∠2,
∵2∠EAF=∠BAD=∠EAD+∠2+∠EAH,
∴∠EAF=∠EAH,
又∵AE=AE,
∴△AEF≌△AEH,
∴EF=EH=BE-BH=BE-DF,即EF=BE-DF,
∴①中的结论不成立.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案