题目内容
【题目】如图,直线y=x+4与x轴、y轴分别交于点A和点B,点D为线段OB的中点,点C、P分别为线段AB、OA上的动点,当PC+PD值最小时点P的坐标为_______
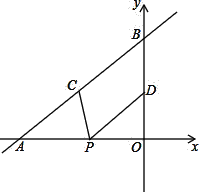
【答案】P(-2,0)
【解析】
先作点D关于x轴的对称点D′,过点D′作D′C⊥AB垂足为C,线段D′C交x轴于点P,此时可知P D′=PD,因此PC+PD= PC+P D′=C D′,此时利用直线外一点到已知线段垂线段最短,此时PC+PD值最小,再由函数与坐标轴的交点坐标求出角度关系即可求出答案.
解:作点D关于x轴的对称点D′,过点D′作D′C⊥AB垂足为C,线段D′C交x轴于点P,连接PD,由轴对称的基本性质,可知P D′=PD,
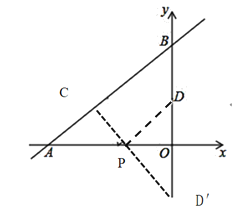
∴PC+PD= PC+P D′=C D′,此时直线外一点到已知线段垂线段最短,此时PC+PD值最小.
令一次函数y=x+4中x=0,则y=4,
∴点B的坐标为(0,4);
所以D(0,2),则D′(0,-2),OD′=2
令y=x+4中y=0,则
x+4=0,解得:x=-4,
∴点A的坐标为(-4,0).
∴OA=OB
∴∠CBD=45°
又∵D′C⊥AB垂直为C
∴∠O D′P=45°
又∵x轴⊥y轴
∴∠OP D′=∠O D′P=45°
∴OP=OD′=2
∴P(-2,0)
故填:(-2,0)

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目