Question

【题目】如图，已知正方形ABCD的边长为6，点E、F分别在BC、DC上，CE=DF=2，DE与AF相交于点G，点H为AE的中点，连接GH．

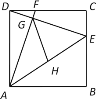
（1）求证：△ADF≌△DCE；

（2）求GH的长．

Answer 1

【答案】（1）详见解析；（2）

【解析】

（1）根据正方形的性质可得AD=DC，∠ADC=∠C=90°，然后即可利用SAS证得结论；

（2）根据全等三角形的性质和余角的性质可得∠DGF=90°，根据勾股定理易求得AE的长，然后根据直角三角形斜边中线的性质即得结果．

（1）证明：∵四边形ABCD是正方形，

∴AD=DC，∠ADC=∠C=90°，

∵DF = CE，

∴△ADF≌△DCE（SAS）；

（2）解：∵△ADF≌△DCE，∴∠DAF=∠CDE，

∵∠DAF+∠DFA=90°，∴∠CDE +∠DFA=90°，

∴∠DGF=90°，∴∠AGE=90°，

∵AB=BC=6，EC=2，∴BE=4，

∵∠B=90°，∴AE==，

∵点H为AE的中点，∴GH=．