题目内容
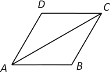
【题目】如图，菱形ABCD中，对角线AC等于
，∠D=120°，则菱形ABCD的面积为（ ）
A.
B.54C.36D.
【答案】D
【解析】
如图，连接BD交AC于点O，根据菱形的性质和等腰三角形的性质可得AO的长、BO=DO、AC⊥BD、∠DAC =30°，然后利用30°角的直角三角形的性质和勾股定理可求出OD的长，即得BD的长，再根据菱形的面积=对角线乘积的一半计算即可.
解：如图，连接BD交AC于点O，∵四边形ABCD是菱形，
∴AD=CD，AO=CO=
，BO=DO，AC⊥BD，
∵∠ADC=120°，∴∠DAC=∠ACD=30°，∴AD=2DO，
设DO=x，则AD=2x，在直角△ADO中，根据勾股定理，得
，解得：x=3，（负值已舍去）∴BD=6，
∴菱形ABCD的面积=
．
故选：D．
练习册系列答案
每课必练系列答案
巧学巧练系列答案
相关题目
