题目内容
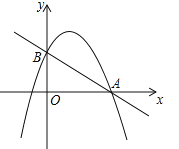
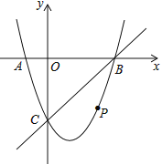
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() 点在原点的左侧,
点在原点的左侧,![]() 点的坐标为(
点的坐标为(![]() ,
,![]() ),与
),与![]() 轴交于
轴交于![]() (
(![]() ,
,![]() ),点
),点![]() 是直线
是直线![]() 下方的抛物线上一动点.
下方的抛物线上一动点.
(1)求这个二次函数的表达式.
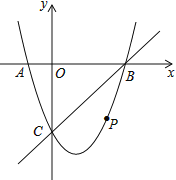
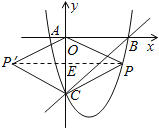
(2)连结![]() 、
、![]() ,并把△
,并把△![]() 沿
沿![]() 边翻折,得到四边形
边翻折,得到四边形![]() , 那么是否存在点
, 那么是否存在点![]() ,使四边形
,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 的面积最大并求出此时
的面积最大并求出此时![]() 点的坐标和四边形
点的坐标和四边形![]() 的最大面积.
的最大面积.
【答案】(1)y=x2-2x-3;(2)存在, ;(3)当点P的坐标为
;(3)当点P的坐标为![]() ,四边形
,四边形![]() 的面积最大,最大面积是
的面积最大,最大面积是![]()
【解析】
(1)将B、C的坐标代入抛物线的解析式中即可求得待定系数的值;.
(2)由于菱形的对角线互相垂直平分,若四边形POP′C为菱形,那么P点必在OC的垂直平分线上,据此可求出P点的纵坐标,代入抛物线的解析式中即可求出P点的坐标;.
(3)由于△ABC的面积为定值,当四边形ABPC的面积最大时,△BPC的面积最大;过P作y轴的平行线,交直线BC于Q,交x轴于F,易求得直线BC的解析式,可设出P点的横坐标,然后根据抛物线和直线BC的解析式求出Q、P的纵坐标,即可得到PQ的长,以PQ为底,B点横坐标的绝对值为高即可求得△BPC的面积,由此可得到关于四边形ACPB的面积与P点横坐标的函数关系式,根据函数的性质即可求出四边形ABPC的最大面积及对应的P点坐标.
(1)将B、C两点的坐标代入![]() ,
,
得![]() ,解得
,解得![]() ,
,
∴二次函数的解析式为y=x22x3;
(2)存在点P,使四边形POP′C为菱形,
设P点坐标为(x,x2-2x-3),PP′交CO于E,
若四边形POP′C是菱形,则有PC=PO,
连接PP′,则PE⊥CO于E,
 .
.
∵C(0,-3),
∴CO=3,
又∵OE=EC,
∴OE=EC=![]() ,
,
∴y=![]() ;
;
∴x2-2x-3=![]() ,
,
解得x1=![]() ,x2=
,x2=![]() (不合题意,舍去),
(不合题意,舍去),
∴存在这样的点,此时P点的坐标为 ;
;
(3)过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(x,x2-2x-3),
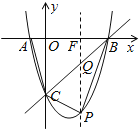
设直线BC的解析式为:y=kx+d,
则![]() ,
,
解得:![]()
∴直线BC的解析式为y=x-3,
则Q点的坐标为(x,x-3),
当0=x2-2x-3,
解得:x1=-1,x2=3,
∴AO=1,AB=4,
S四边形ABPC=S△ABC+S△BPQ+S△CPQ
=![]() ABOC+
ABOC+![]() QPBF+
QPBF+![]() QPOF
QPOF
=![]() ×4×3+
×4×3+![]() (x2+3x)×3
(x2+3x)×3
=![]() (x
(x![]() )2+
)2+![]()
当x=![]() 时,四边形ABPC的面积最大,
时,四边形ABPC的面积最大,
此时P点的坐标为(![]() ,
,![]() ),四边形ABPC的面积的最大值为
),四边形ABPC的面积的最大值为![]() .
.

【题目】把一枚木质中国象棋子“兵”从一定高度落下,落地后“兵”字面可能朝上,也可能朝下.为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验数据如下表:
实验次数 | 20 | 60 | 100 | 120 | 140 | 160 | 500 | 1000 | 2000 | 5000 |
“兵”字面朝上次数 | 14 | 38 | 52 | 66 | 78 | 88 | 280 | 550 | 1100 | 2750 |
“兵”字面朝上频率 | 0.7 | 0.63 | 0.52 | 0.55 | 0.56 | 0.55 | 0.56 | 0.55 | 0.55 | 0.55 |
下面有三个推断:①投掷1000次时,“兵”字面朝上的次数是550,所以“兵”字面朝上的概率是0.55;②随着实验次数的增加,“兵”字面朝上的频率总在0.55附近,显示出一定的稳定性,可以估计“兵”字面上的概率是0.55;③当实验次数为200次时,“兵”字面朝上的频率一定是0.55.其中合理的是______.(填序号①、②、③)