Question

【题目】如图，抛物线y=ax2+bx+c（a≠0）与x轴、y轴分别交于A（﹣1，0）、B（3，0）、C（0，3）三点．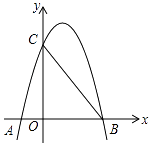

（1）试求抛物线的解析式；
（2）P是直线BC上方抛物线上的一个动点，设P的横坐标为t，P到BC的距离为h，求h与t的函数关系式，并求出h的最大值．
（3）设点M是x轴上的动点，在平面直角坐标系中，是否存在点N，使得以点A、C、M、N为顶点的四边形是菱形？若存在，求出所有符合条件的点N坐标；若不存在，说明理由．

Answer 1

【答案】
（1）

解：∵抛物线y=ax2+bx+c过A（﹣1，0）、B（3，0）、C（0，3）三点，

∴ ，解得 ，

∴抛物线的解析式为y=﹣x2+2x+3；

（2）

解：过点P作PD⊥x轴于点D，交BC于点E，PH⊥BC于点H，连结PB、PC．

∵B（3，0）、C（0，3），

∴OB=OC=3， ，

设直线BC解析式为y=kx+n，则 ，解得 ，

∴直线BC解析式为y=﹣x+3，

∵点P的横坐标为t，且在抛物线y=﹣x2+2x+3上，

∴P（t，﹣t2+2t+3），

又∵PD⊥x轴于点D，交BC于点E，

∴D（t，0），E（t，﹣t+3），

∴PE=（﹣t2+2t+3）﹣（﹣t+3）=﹣t2+3t，

∴ = ，

又∵ ，

∴ ，

∴h与t的函数关系式为： （0＜t＜3），

∵ ，

∴当 时，h有最大值为

（3）

解：存在．

若AM为菱形对角线，则AM与CN互相垂直平分，

∴N（0，﹣3）；

若CM为菱形对角线，则 ，

∴ 或 ；

若AC为菱形对角线，则CN=AM=CM，

设M（m，0），由CM2=AM2，得m2+32=（m+1）2，解得m=4，

∴CN=AM=CM=5，

∴N（﹣5，3）．

综上可知存在点N，使得以点A、C、M、N为顶点的四边形是菱形，符合条件的点N有4个：N1（0，﹣3）， ， ，N4（﹣5，3）

【解析】（1）由A、B、C三点的坐标，利用待定系数法可求得抛物线的解析式；（2）过点P作PD⊥x轴于点D，交BC于点E，PH⊥BC于点H，连结PB、PC，可先求得直线BC的解析式，则可用t分别表示出E的坐标，从而可表示出PE的长，再可用t表示出△PBC的面积，再利用等积法可用t表示出h，利用二次函数的性质可求得h的最大值；（3）分AM、CM和AC为对角线三种情况，分别根据菱形的性质可求得N点的坐标．