题目内容
【题目】如图所示,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24 ㎝,BC=26㎝,动点P从点A开始沿AD边以每秒1㎝的速度向D点运动,动点Q从点C开始沿CB边以每秒3㎝的速度向B运动,P,Q分别从A,C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t s.
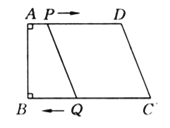
(1)t为何值时,四边形PQCD为平行四边形?
(2)t为何值时,四边形PQCD为等腰梯形?
(3)t为何值时,四边形ABQP为矩形?
【答案】(1)t=6时;(2)t=7时;(3)t=![]() 时.
时.
【解析】试题分析:(1)要使四边形PQCD是平行四边形,则点在运动的过程中,只需PD=QC就满足题意;
(2)作DE⊥BC,PF⊥BC,垂足分别为E,F,要使四边形PQCD为等腰梯形,则QF=CE;依此即可求解;
(3)要使四边形ABQP为矩形,则点在运动的过程中,只需AP=BQ就满足题意.
试题解析:解:由已知得AP=t,CQ=3t,PD=24-t,BQ=26-3t.
(1)∵PD∥CQ,∴当PD=CQ时,即3t=24-t时,四边形PQCD为平行四边形,解得t=6.故当t=6时,四边形PQCD为平行四边形.
(2)如图所示,作DE⊥BC,PF⊥BC,垂足分别为E,F,则CE=2.当QF=CE时,即QF+CE=2CE=4时,四边形PQCD是等腰梯形.此时有CQ-EF=4,即3t—(24一t)=4,解得t=7.故当t=7时,四边形PQCD为等腰梯形.
(3)若四边形ABQP为矩形,则AP=BQ,即t=26—3t,解得t=![]() .故当t=
.故当t=![]() 时,四边形ABQP为矩形.
时,四边形ABQP为矩形.


练习册系列答案
相关题目