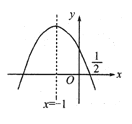
题目内容
【题目】甲经销商库存有1200套A品牌服装,每套进价400元,售价500元,一年内可卖完.现市场流行B品牌服装,每套进价300元,售价600元,但一年内只允许经销商一次性订购B品牌服装,一年内B品牌服装销售无积压,因甲经销商无流动资金可用,只有低价转让A品牌服装,转让来的资金全部用于购进B品牌服装,并销售。经与乙经销商协商,甲、乙双方达成转让协议,转让价格y(元/套)与转让数量x(套)之间的函数关系式为![]() (
(![]() ),若甲经销商转让x套A品牌服装,一年内所获总利润为W(元).
),若甲经销商转让x套A品牌服装,一年内所获总利润为W(元).
(1)求转让后剩余的A品牌服装的销售款![]() (元)与x(套)之间的函数关系式;
(元)与x(套)之间的函数关系式;
(2)求B品牌服装的销售款![]() (元)与x(套)之间的函数关系式;
(元)与x(套)之间的函数关系式;
(3)求W(元)与x(套)之间的函数关系式,当转让多少套时,所获总利润W最大?最大值是多少?
【答案】(1)Q1=-500x+600000(100≤x≤1200);(2)Q2=-![]() x2+720x(100≤x≤1200);(3)W=-
x2+720x(100≤x≤1200);(3)W=-![]() (x-550)2+180500(100≤x≤1200);当x=550时,W有最大值,最大值为180500元.
(x-550)2+180500(100≤x≤1200);当x=550时,W有最大值,最大值为180500元.
【解析】
(1)直接根据销售款=售价×套数即可得出结论;
(2)先表示出转让总金额,再表示出购买B服装的套数,再与售价相乘即可;
(3)把(1)(2)中的销售款相加再减去成本即可.
解:(1)∵甲经销商库存有1200套A品牌服装,每套售价500元,转让x套给乙,
∴Q1=500×(1200-x)=-500x+600000(100≤x≤1200);
(2)∵转让价格y(元/套)与转让数量x(套)之间的函数关系式为![]() (100≤x≤1200),B品牌服装,每套进价300元,
(100≤x≤1200),B品牌服装,每套进价300元,
∴转让后可购买B服装的套数 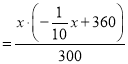 =
=![]() ,
,
∴Q2=(![]() )×600=-
)×600=-![]() x2+720x(100≤x≤1200);
x2+720x(100≤x≤1200);
(3)∵由(1)、(2)知,Q1=-500x+600000,Q2=-![]() x2+720x,
x2+720x,
∴W=Q1+Q2-400×1200
=-500x+600000-![]() x2+720x-480000
x2+720x-480000
=-![]() x2+220x+120000
x2+220x+120000
=-![]() (x-550)2+180500,
(x-550)2+180500,
∴W=-![]() (x-550)2+180500(100≤x≤1200),
(x-550)2+180500(100≤x≤1200),
∴当x=550时,W有最大值,最大值为180500元.