题目内容
【题目】如图,抛物线y=x2﹣4x与x轴交于点O,A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( ) 
A.4
B.8
C.16
D.32
【答案】B
【解析】解:当y=0时,x2﹣4x=0,解得x1=0,x2=4,则A(4,0),
∵y=x2﹣4x=(x﹣2)2﹣4,
∴B(2,﹣4),
设直线AB的解析式为y=kx+b,
把A(4,0),B(2,﹣4)代入得 ![]() ,解得
,解得 ![]() ,
,
∴直线AB的解析式为y=2x﹣8;
当x=0时,y=2x﹣8=﹣8,则C(0,﹣8),
∴图中阴影部分的面积和=S△OBC= ![]() ×8×2=8.
×8×2=8.
故选B.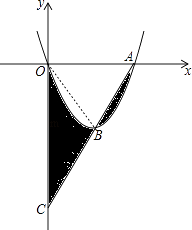
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目