题目内容
【题目】已知二次函数![]() (其中b,c为常数,c>0)的顶点恰为函数
(其中b,c为常数,c>0)的顶点恰为函数![]() 和
和![]() 的其中一个交点.则当
的其中一个交点.则当![]() >
>![]() >
>![]() 时,a的取值范围是 .
时,a的取值范围是 .
【答案】-1<a<0或a>3.
【解析】
试题分析:本题主要考查了直线与反比例函数图象的交点、抛物线的顶点坐标公式、直线与抛物线的交点等知识,运用数形结合的思想是解决本题的关键.只需先求出抛物线的顶点坐标,再求出抛物线与直线y=2x的交点,然后结合函数图象就可解决问题.
解方程组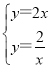 ,得
,得
![]() ,
,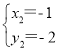 .
.
①当抛物线y=x2+bx+c顶点为(1,2)时,抛物线的解析式为y=(x-1)2+2=x2-2x+3.
解方程组得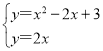 ,
,![]() ,
,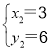 .
.
结合图象可得:
当a2+ab+c>2a>2a时,a的取值范围是-1<a<0或a>3;
②当抛物线y=x2+bx+c顶点为(-1,-2)时,
抛物线的解析式为y=(x+1)2-2=x2+2x-1.
∴c=-1<0,与条件c>0矛盾,故舍去.
故答案为-1<a<0或a>3.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表: 频数分布表
身高分组 | 频数 | 百分比 |
x<155 | 5 | 10% |
155≤x<160 | a | 20% |
160≤x<165 | 15 | 30% |
165≤x<170 | 14 | b |
x≥170 | 6 | 12% |
总计 | 100% |
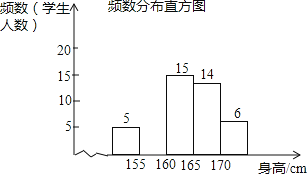
(1)填空:a= ,b= ;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?