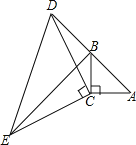
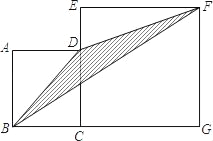
[题目]如图.四边形ABCD和四边形EFBC均为正方形.点D在EC上．如果线段AB的长为5.则△BDF的面积为．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，四边形ABCD和四边形EFBC均为正方形，点D在EC上．如果线段AB的长为5，则△BDF的面积为_____．

【答案】12.5

【解析】

设出正方形EFCG的边长为a，表示出ED与BG，求出三角形EFD的面积，由正方形EFCG的面积-三角形EFD的面积得到四边形DCGF的面积，求出三角形BCD的面积，三角形BDF面积=三角形BCD面积+四边形DCGF的面积-三角形BGF的面积，求出即可．

设正方形EFGC的边长为a，即EC=EF=CG=FG=a，

∴ED=ECDC=a5，BG=BC+CG=a+5，

∴S△EFD=12a(a5)，

∴S四边形DCGF=a212a(a5)，

∵S△BCD=12×52=12.5,S△BCF=12a(a+5)，

∴S△BDF=S△BCD+S四边形DCGFS△BCF=12.5+a212a(a5)12a(a+5)=12.5，

故答案为：12.5.

练习册系列答案

（1）求证：△ACD≌△BCE；

（2）若AB=2cm，则BE=_______cm．

（3）BE与AD有何位置关系？请说明理由．

【题目】如图，在正方形ABCD中，E、F分别是边AD、CD上的点，AE=ED，DF= DC，连接EF并延长交BC的延长线于点G．
（1）求证：△ABE∽△DEF；
（2）若正方形的边长为4，求BG的长．

【题目】在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．

（1）如图1，当点D在线段BC上，如果∠BAC=90，则∠BCE 度；

（2）设∠BAC=，∠BCE=．

①如图2，当点D在线段BC上移动，则，之间有怎样的数量关系？请说明理由；

②当点D在直线BC上移动，则，之间有怎样的数量关系？请直接写出你的结论，不必说明理由．

【题目】某工程队修建一条长1200m的道路，采用新的施工方式，工效提升了50%，结果提前4天完成任务．
（1）求这个工程队原计划每天修建道路多少米？
（2）在这项工程中，如果要求工程队提前2天完成任务，那么实际平均每天修建道路的工效比原计划增加百分之几？

【题目】如图，BD是正方形ABCD的对角线，BC=2，边BC在其所在的直线上平移，将通过平移得到的线段记为PQ，连接PA、QD，并过点Q作QO⊥BD，垂足为O，连接OA、OP．

（1）请直接写出线段BC在平移过程中，四边形APQD是什么四边形？
（2）请判断OA、OP之间的数量关系和位置关系，并加以证明；
（3）在平移变换过程中，设y=S△OPB ， BP=x（0≤x≤2），求y与x之间的函数关系式，并求出y的最大值．

【题目】如图，正方形ABCD的边长为1，AC，BD是对角线．将△DCB绕着点D顺时针旋转45°得到△DGH，HG交AB于点E，连接DE交AC于点F，连接FG．
则下列结论：
①四边形AEGF是菱形
②△AED≌△GED
③∠DFG=112.5°
④BC+FG=1.5
其中正确的结论是．

【题目】已知四边形ABCD是正方形，等腰直角△AEF的直角顶点E在直线BC上（不与点B，C重合），FM⊥AD，交射线AD于点M．

（1）当点E在边BC上，点M在边AD的延长线上时，如图①，求证：AB+BE=AM；
（提示：延长MF，交边BC的延长线于点H．）
（2）当点E在边CB的延长线上，点M在边AD上时，如图②；当点E在边BC的延长线上，点M在边AD上时，如图③．请分别写出线段AB，BE，AM之间的数量关系，不需要证明；
（3）在（1），（2）的条件下，若BE=，∠AFM=15°，则AM=.

【题目】如图，已知一个直角三角形纸片ACB，其中∠ACB=90°，AC=4，BC=3，E、F分别是AC、AB边上点，连接EF．

（1）图①，若将纸片ACB的一角沿EF折叠，折叠后点A落在AB边上的点D处，且使S四边形ECBF=3S△EDF ，求AE的长；
（2）如图②，若将纸片ACB的一角沿EF折叠，折叠后点A落在BC边上的点M处，且使MF∥CA．
①试判断四边形AEMF的形状，并证明你的结论；
②求EF的长；
（3）如图③，若FE的延长线与BC的延长线交于点N，CN=1，CE= ，求的值．

试题分类