Question

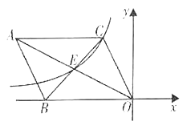
【题目】如图，为了测量建筑物CD、EF的高度，在直线CE上选取观测点A、B，AC的距离为40米．从A、B测得建筑物的顶部D的仰角分别为51.34°、68.20°，从B、D测得建筑物的顶部F的仰角分别为64.43°、26.57°．

（1）求建筑物CD的高度；

（2）求建筑物EF的高度．

（参考数据：tan51.34°≈1.25，tan68.20°≈2.5，tan64.43°≈2，tan26.57°≈0.5）

Answer 1

【答案】（1）建筑物CD的高度为50米；（2）建筑物EF的高度为80米．

【解析】

（1）在Rt△ACD中，∠ACD＝90°，tan∠DAC＝，即可得到结果；

（2）过点D作DG⊥EF于点G ，证明四边形DCEG是矩形，得到CD＝EG＝50，DG＝CE，根据Rt△DFG可求出DG，根据Rt△FBE求出BE，即可得到结果．

解：（1）在Rt△ACD中，∠ACD＝90°，

∵tan∠DAC＝，

∴CD＝AC·tan51.34°≈40×1.25＝50．

（2）过点D作DG⊥EF于点G．

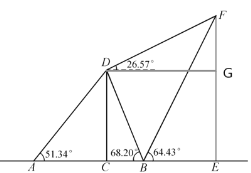
在Rt△BCD中，∠BCD＝90°，

∵tan∠DBC＝，

∴BC＝．

根据,,,可得四边形DCEG是矩形，

∴CD＝EG＝50，DG＝CE．

设EF＝x米．

在Rt△DFG中，∠DGF＝90°，

∵tan∠FDG＝，

∴DG＝，

在Rt△FBE中，∠BEF＝90°，

∵tan∠FBE＝，

∴BE＝，

∴＝20＋，

∴x≈80．

答：建筑物CD的高度为50米，建筑物EF的高度为80米．