Question

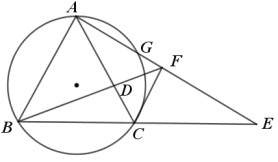
【题目】如图，PQ、PB、QC是⊙O的切线，切点分别为A、B、C，点D在上，若∠D＝100°，则∠P与∠Q的度数之和是（ ）

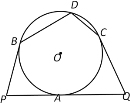
A.160°B.140°C.120°D.100°

Answer 1

【答案】A

【解析】

根据圆周角定理和切线的性质以及三角形的内角和定理即可得到结论．

连接OA，OB，OC，AB，AC，

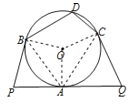
∵∠D＝100°，

∴∠BAC＝180°∠D＝80°，

∴∠BOC＝2∠BAC＝160°，

∴∠AOB＋∠AOC＝360°160°＝200°，

∵PQ、PB、QC是⊙O的切线，

∴∠PBO＝∠PAO＝∠QAO＝∠QCO＝90°，

∴∠P＋∠Q＝2×360°∠PBO∠PAO∠QAO∠QCO∠AOB∠AOC＝720°4×90°200°＝160°，

故选：A．