��Ŀ����
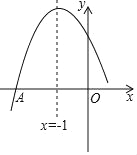
����Ŀ����ͼ��������y1=ax2+bx+c��a��0��ͼ���һ���֣��䶥������ΪA����1����3������x���һ������ΪB����3��0����ֱ��y2=mx+n��m��0���������߽���A��B���㣬���н��ۣ���abc��0���ڲ���ʽax2+��b��m��x+c��n��0�Ľ⼯Ϊ��3��x����1������������x�����һ�������ǣ�3��0�����ܷ���ax2+bx+c+3=0��������ȵ�ʵ������������ȷ���ǣ�������
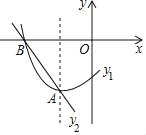
A. �٢� B. �ڢ� C. �ۢ� D. �ڢ�
���𰸡�D
��������
�ٴ���������a��0��b��0��c��0��abc��0��
����ȷ����Ϊy1=ax2+bx+c��a��0��ͼ����ֱ��y2=mx+n��m��0������A��B���㣬��ax2+bx+c��mx+nʱ��-3��x��-1��������ʽax2+��b-m��x+c-n��0�Ľ⼯Ϊ-3��x��-1���ʢ���ȷ��
�۴�����������x�����һ�������ǣ�1��0����
����ȷ��������y1=ax2+bx+c��a��0��ͼ����ֱ��y=-3ֻ��һ�����㣬����ax2+bx+c+3=0��������ȵ�ʵ�������ʢ���ȷ��
�⣺�������߿������ϣ���a��0��
�������߽�y���ڸ����ᣬ��c��0��
�߶Գ�����y����ߣ���-![]() ��0��
��0��
��b��0��
��abc��0���ʢٴ���
��y1=ax2+bx+c��a��0��ͼ����ֱ��y2=mx+n��m��0������A��B���㣬
��ax2+bx+c��mx+nʱ��-3��x��-1��
������ʽax2+��b-m��x+c-n��0�Ľ⼯Ϊ-3��x��-1���ʢ���ȷ��
��������x�����һ�������ǣ�1��0�����ʢ۴���
��������y1=ax2+bx+c��a��0��ͼ����ֱ��y=-3ֻ��һ�����㣬
���ax2+bx+c+3=0��������ȵ�ʵ�������ʢ���ȷ��
��ѡ��D��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�