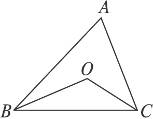
题目内容
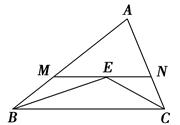
已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC,
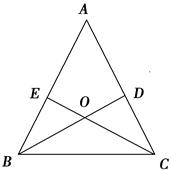
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由.

(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由.
见解析
(1)证明:∵OB=OC,∴∠OBC=∠OCB,
∵锐角△ABC的两条高BD、CE相交于点O,
∴∠BEC=∠BDC=90°,
∵∠BEC+∠BCE+∠ABC=∠BDC+∠DBC
+∠ACB=180°,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形;
(2)解:连接AO并延长交BC于E,

∵AB=AC,OB=OC,∴AE是BC的垂直平分线,
∴∠BAE=∠CAE,∴点O在∠BAC的角平分线上.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
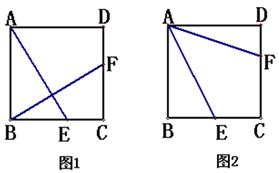
 , AE的长为
, AE的长为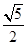 ,试求AF的长度。
,试求AF的长度。