题目内容
已知边长为1的正方形ABCD中,点E、F分别在边BC、CD上,
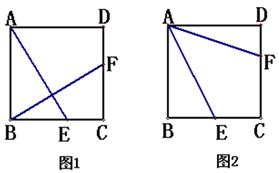
(1)如图1,若AE⊥BF,求证:EA=FB;
(2)如图2,若∠EAF=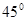 , AE的长为
, AE的长为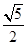 ,试求AF的长度。
,试求AF的长度。

(1)如图1,若AE⊥BF,求证:EA=FB;
(2)如图2,若∠EAF=
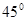 , AE的长为
, AE的长为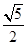 ,试求AF的长度。
,试求AF的长度。(1)证明见解析;(2)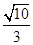 .
.
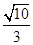 .
.试题分析:(1)根据正方形的性质,得到∠ABE=∠BCF=90°,AB=BC,进而得到∠BAE=∠CBF,则△ABE≌△BCF,进一步根据全等三角形的性质进行证明;
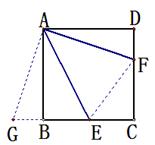
(2)延长CB至点G,使BG=DF,并连接AG和EF,先证△ABG≌△ADF(SAS),再证△AEG≌△AEF(SAS);在RT△ABE中,根据勾股定理可求得BE=
 ,设线段DF长为x,则EF=GE=x+
,设线段DF长为x,则EF=GE=x+ ,又CE=1-
,又CE=1- =
= ,CF=1-x,最终在RT△ECF中,利用勾股定理得(
,CF=1-x,最终在RT△ECF中,利用勾股定理得( +x)2=
+x)2=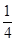 +(1?x)2,求得x=
+(1?x)2,求得x=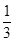 ,在Rt△ADF中,解得AF=
,在Rt△ADF中,解得AF= .
. 试题解析:(1)证明:∵四边形ABCD是正方形,AE⊥BF,
∴∠BAE+∠ABM=90°,∠CBF+∠ABM=90°,
∴∠BAE=∠CBF,
在△ABE和△BCF中,
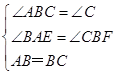 ,
,∴△ABE≌△BCF(AAS),
∴AE=BF;
(2)延长CB至点G,使BG=DF,并连接AG和EF,先证⊿ABG≌⊿ADF(SAS),再证⊿AEG≌⊿AEF(SAS);在RT⊿ABE中,根据勾股定理可求得BE=
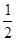 ,设线段DF长为x,则EF=GE=x+
,设线段DF长为x,则EF=GE=x+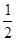 ,又CE=1-
,又CE=1-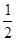 =
=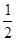 ,CF=1-x,最终在RT⊿ECF中,利用勾股定理得
,CF=1-x,最终在RT⊿ECF中,利用勾股定理得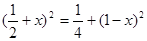 ,求得x=
,求得x=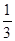 ,在
,在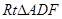 中,解得
中,解得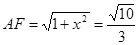
考点: 1.正方形的性质;2.全等三角形的判定与性质;3.勾股定理.

练习册系列答案
相关题目