题目内容
【题目】在平面直角坐标系中,规定:抛物线y=a(xh) ![]() +k的关联直线为y=a(xh)+k.
+k的关联直线为y=a(xh)+k.
例如:抛物线y=2(x+1) ![]() 3的关联直线为y=2(x+1)3,即y=2x1.
3的关联直线为y=2(x+1)3,即y=2x1.
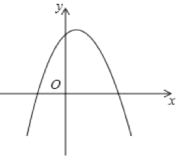
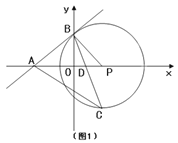
(1)如图,对于抛物线y=(x1) ![]() +3.
+3.
①该抛物线的顶点坐标为___,关联直线为___,该抛物线与其关联直线的交点坐标为___和___;
②点P是抛物线y=(x1) ![]() +3上一点,过点P的直线PQ垂直于x轴,交抛物线y=(x1)
+3上一点,过点P的直线PQ垂直于x轴,交抛物线y=(x1)![]() +3的关联直线于点Q.设点P的横坐标为m,线段PQ的长度为d(d>0),求当d随m的增大而减小时,d与m之间的函数关系式,并写出自变量m的取值范围。
+3的关联直线于点Q.设点P的横坐标为m,线段PQ的长度为d(d>0),求当d随m的增大而减小时,d与m之间的函数关系式,并写出自变量m的取值范围。
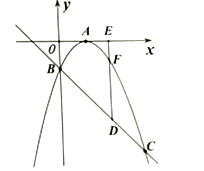
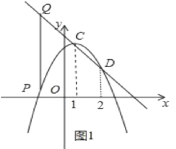
(2)顶点在第一象限的抛物线y=a(x1) ![]() +4a与其关联直线交于点A,B(点A在点B的左侧),与x轴负半轴交于点C,直线AB与x轴交于点D,连结AC、BC.
+4a与其关联直线交于点A,B(点A在点B的左侧),与x轴负半轴交于点C,直线AB与x轴交于点D,连结AC、BC.
①求△BCD的面积(用含a的代数式表示).
②当△ABC为钝角三角形时,直接写出a的取值范围。
【答案】(1)①(1,3),y=x+4,(1,3)和(2,2);②当m<1,d=m![]() 3m+2;
3m+2; ![]() m<2时,d=m
m<2时,d=m![]() +3m2;;(2)①9a;②0<a<
+3m2;;(2)①9a;②0<a<![]() 或a>1.
或a>1.
【解析】
(1)①利用二次函数的性质和新定义得到抛物线的顶点坐标和关联直线解析式;然后解方程组![]() 得该抛物线与其关联直线的交点坐标;
得该抛物线与其关联直线的交点坐标;
②设P(m,-m![]() +2m+2),则Q(m,-m+4),如图1,利用d随m的增大而减小得到m<1或1<m<2,当m<1时,用m表示s得到d=m
+2m+2),则Q(m,-m+4),如图1,利用d随m的增大而减小得到m<1或1<m<2,当m<1时,用m表示s得到d=m![]() -3m+2;当1<m<2时,利用m表示d得到d=-m
-3m+2;当1<m<2时,利用m表示d得到d=-m![]() +3m-2,根据二次函数的性质得当m≥
+3m-2,根据二次函数的性质得当m≥![]() ,d随m的增大而减小,所以
,d随m的增大而减小,所以![]() ≤m<2时,d=-m
≤m<2时,d=-m![]() +3m-2;
+3m-2;
(2)①先确定抛物线y=-a(x-1)![]() +4a的关联直线为y=-ax+5a,再解方程组
+4a的关联直线为y=-ax+5a,再解方程组
![]() 得A(1,4a),B(2,3a),接着解方程-a(x-1)
得A(1,4a),B(2,3a),接着解方程-a(x-1)![]() +4a=0得C(-1,0),解方程-ax+5a=0得D(5,0),然后利用三角形面积公式求解;
+4a=0得C(-1,0),解方程-ax+5a=0得D(5,0),然后利用三角形面积公式求解;
②利用两点间的距离公式得到AC![]() =2
=2![]() +16a
+16a![]() ,BC
,BC![]() =3
=3![]() +9a
+9a![]() ,AB
,AB![]() =1
=1![]() +a
+a![]() ,讨论:当AC
,讨论:当AC![]() +AB
+AB![]() <BC
<BC![]() ,∠BAC为钝角,即2
,∠BAC为钝角,即2![]() +16a
+16a![]() +1
+1![]() +a
+a![]() <3
<3![]() +9a
+9a![]() ;当BC
;当BC![]() +AB
+AB![]() <AC
<AC![]() ,∠BAC为钝角,即3
,∠BAC为钝角,即3![]() +9a
+9a![]() +1
+1![]() +a
+a![]() <2
<2![]() +16a
+16a![]() ,然后分别解不等式即可得到a的范围.
,然后分别解不等式即可得到a的范围.
(1)①抛物线的顶点坐标为(1,3),关联直线为y=(x1)+3=x+4,
解方程组![]() 得
得![]() 或
或![]() ,
,
所以该抛物线与其关联直线的交点坐标为(1,3)和(2,2);
故答案为(1,3),y=x+4,(1,3)和(2,2);
②设P(m,m![]() +2m+2)则Q(m,m+4),如图1,
+2m+2)则Q(m,m+4),如图1,
∵d随m的增大而减小,
∴m<1或1<m<2,
当m<1时,d=m+4(m![]() +2m+2)=m
+2m+2)=m![]() 3m+2;
3m+2;
当1<m<2时,d=m![]() +2m+2(m+4)=m
+2m+2(m+4)=m![]() +3m2,当m
+3m2,当m![]() ,d随m的增大而减小,
,d随m的增大而减小,
综上所述,当m<1,d=m![]() 3m+2;
3m+2; ![]() m<2时,d=m
m<2时,d=m![]() +3m2;
+3m2;
(2)①抛物线y=a(x1) ![]() +4a的关联直线为y=a(x1)+4a=ax+5a,
+4a的关联直线为y=a(x1)+4a=ax+5a,
解方程组![]() 得
得![]() 或
或![]() ,
,
∴A(1,4a),B(2,3a),
当y=0时,a(x1) ![]() +4a=0,解得x
+4a=0,解得x![]() =3,x
=3,x![]() =1,则C(1,0),
=1,则C(1,0),
当y=0时,ax+5a=0,解得x=5,则D(5,0),
∴S△BCD=![]() ×6×3a=9a;
×6×3a=9a;
②AC![]() =2
=2![]() +16a
+16a![]() ,BC
,BC![]() =3
=3![]() +9a
+9a![]() ,AB
,AB![]() =1
=1![]() +a
+a![]() ,
,
当AC![]() +AB
+AB![]() <BC
<BC![]() ,∠BAC为钝角,即2
,∠BAC为钝角,即2![]() +16a
+16a![]() +1
+1![]() +a
+a![]() <3
<3![]() +9a
+9a![]() ,解得a<
,解得a<![]() ;
;
当BC![]() +AB
+AB![]() <AC
<AC![]() ,∠BAC为钝角,即3
,∠BAC为钝角,即3![]() +9a
+9a![]() +1
+1![]() +a
+a![]() <2
<2![]() +16a
+16a![]() ,解得a>1,
,解得a>1,
综上所述,a的取值范围为0<a<![]() 或a>1
或a>1

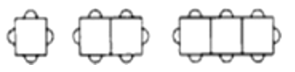
【题目】按下图方式摆放餐桌和椅子,
 …
…
(1)1张长方形餐桌可坐4人,2张长方形餐桌拼在一起可坐______人.
(2)按照上图的方式继续排列餐桌,完成下表.
桌子张数 | 3 | 4 | 5 | n |
可坐人数 | ______ | ______ | ______ | ______ |
(3)一家餐厅有40张这样的长方形餐桌,某用餐单位要求餐厅按照上图方式,每8张长方形餐桌拼成1张大桌子,则该餐厅此时能容纳多少人用餐?
【题目】如图,将一张正方形纸片剪成四张大小一样的小正方形纸片,然后将其中一张正方形纸片再按同样方法剪成四张小正方形纸片,再将其中一张剪成四张小正方形纸片,如此进行下去.
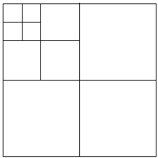
(1)填表:
剪的次数 | 1 | 2 | 3 | 4 | 5 |
纸片张数 | 4 | 7 |
(2)如果剪了100次,共剪出多少张纸片?
(3)如果剪了![]() 次,共剪出多少张纸片?
次,共剪出多少张纸片?
(4)能否剪若干次后共得到2019张纸片?若能,请直接写出相应剪的次数;若不能,请说明理由.