题目内容
【题目】如图,在△ABC中,D、E、F分别是各边的中点,BH是AC边上的高.
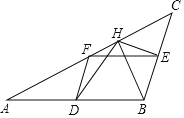
(1)求证:四边形DBEF是平行四边形;(2)求证:∠DFE=∠DHE.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据三角形中位线定理得到DF∥BC,EF∥AB,于是得到结论;
(2)根据平行线的性质得到∠A=∠EFH,再在Rt△ABH中利用直角三角形斜边上的中线等于斜边一半的性质得到DA=DH,于是∠EFH=∠FHD,同理,∠CHE=∠AFD,根据平角的定义即可得到结论.
证明:(1)∵D、E、F分别是各边的中点,
∴DF和EF是△ABC的中位线,
∴DF∥BC,EF∥AB,
∴DF∥BE,EF∥BD,
∴四边形DBEF是平行四边形;
(2)∵EF∥AB,∴∠A=∠EFH,
∵BH⊥AC,∴∠AHB=90°,
∵D为AB的中点,
∴AD=DH,
∴∠AHD=∠A,
∴∠EFH=∠FHD,
同理,∠CHE=∠AFD,
∴∠DFE=∠DHE.

练习册系列答案
相关题目