题目内容
【题目】甲、乙两名自行车爱好者准备在段长为3500米的笔直公路上进行比赛，比赛开始时乙在起点，甲在乙的前面.他们同时出发，匀速前进，已知甲的速度为12米/秒，设甲、乙两人之间的距离为s(米)，比赛时间为t(秒)，图中的折线表示从两人出发至其中一人先到达终点的过程中s(米)与t(秒)的函数关系根据图中信息，回答下列问题：
(1)乙的速度为多少米/秒；
(2)当乙追上甲时，求乙距起点多少米；
(3)求线段BC所在直线的函数关系式.
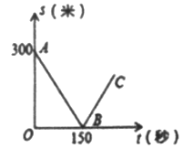
【答案】(1)14；（2）乙距起点2100米；（3）BC所在直线的函数关系式为s=2t-300.
【解析】
（1）设乙的速度为x米/秒，根据图象得到300＋150×12＝150x，解方程即可；
（2）由图象可知乙用了150秒追上甲，用时间乘以速度即可；
（3）先计算出乙完成全程所需要的时间为
＝250（秒），则乙追上甲后又用了250150＝100秒到达终点，所以这100秒他们相距100×（1412）米，可得到C点坐标，而B点坐标为（150，0），然后利用待定系数法求线段BC所在直线的函数关系式即可．
解：(1)设乙的速度为x米/秒，
则300+150×12=150x，
解得x=14，
故答案为：14.
(2)由图象可知乙用了150秒追上甲，14×150=2100(米).
∴当乙追上甲吋，乙距起点2100米.
(3)乙从出发到终点的时间为=250(秒)，
此时甲、乙的距离为：(250-150)(14-12)=200(米)，
∴C点坐标为 (250，200)，B点坐标为(150，0)
设BC所在直线的函数关系式为s=kt+b(k
0，k，b为常数)，
将B、C两点代入，得
，
解得
∴BC所在直线的函数关系式为s=2t-300.
教材全解字词句篇系列答案
【题目】要从甲、乙两名同学中选出一名，代表班级参加射击比赛. 现将甲、乙两名同学参加射击训练的成绩绘制成下列两个统计图：
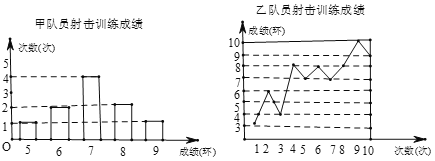
根据以上信息，整理分析数据如下：
平均成绩(环) | 中位数(环) | 众数(环) | 方差( | |
甲 | 7 |
| 7 | 1. 2 |
乙 |
| 7. 5 |
| 4. 2 |
(1)分别求表格中
、
、
的值.
(2)如果其他参赛选手的射击成绩都在7环左右，应该选______队员参赛更适合；如果其他参赛选手的射击成绩都在8环左右，应该选______队员参赛更适合.
