题目内容
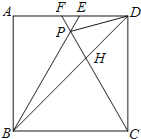
【题目】如图,矩形ABCD中,点E、F分别在AB、BC上,△DEF为等腰直角三角形,∠DEF=90°,AD+CD=10,AE=2,求AD的长.

【答案】AD=4.
【解析】
试题分析:先设AD=x.由△DEF为等腰直角三角形,可以得到一对边相等,一对角相等,再加上一对直角相等,那么△ADE和△BEF全等,就有AD=BE.那么利用边相等可得x+x+2=10,解之即得AD.
解:先设AD=x.
∵△DEF为等腰三角形.
∴DE=EF,∠FEB+∠DEA=90°.
又∵∠AED+∠ADE=90°.
∴∠FEB=∠EDA.
又∵四边形ABCD是矩形,
∴∠B=∠A=90°
∴△ADE≌△BEF(AAS).
∴AD=BE.
∴AD+CD=AD+AB=x+x+2=10.
解得x=4.
即AD=4.

练习册系列答案
相关题目