Question

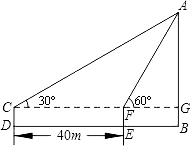
【题目】如图，花丛中有一路灯杆AB．在灯光下，小明在D点处的影长DE=3米，沿BD方向行走到达G点，DG=5米，这时小明的影长GH=5米．如果小明的身高为1.7米，求路灯杆AB的高度（精确到0.1米）．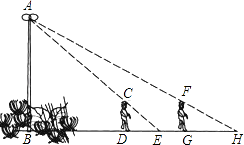

Answer 1

【答案】解：根据题意得：AB⊥BH，CD⊥BH，FG⊥BH， 在Rt△ABE和Rt△CDE中，
∵AB⊥BH，CD⊥BH，
∴CD∥AB，
可证得：
△CDE∽△ABE
∴ ①，
同理： ②，
又CD=FG=1.7m，
由①、②可得：
，
即 ，
解之得：BD=7.5m，
将BD=7.5代入①得：
AB=5.95m≈6.0m．
答：路灯杆AB的高度约为6.0m．
【解析】根据AB⊥BH，CD⊥BH，FG⊥BH，可得：△ABE∽△CDE，则有 和 ，而 ，即 ，从而求出BD的长，再代入前面任意一个等式中，即可求出AB．
【考点精析】通过灵活运用相似三角形的应用，掌握测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解即可以解答此题．