题目内容
【题目】以![]() 的各边,在边
的各边,在边![]() 的同侧分别作三个正方形.他们分别是正方形
的同侧分别作三个正方形.他们分别是正方形![]() ,
,![]() ,
,![]() ,试探究:
,试探究:
![]() 如图中四边形
如图中四边形![]() 是什么四边形?并说明理由.
是什么四边形?并说明理由.
![]() 当
当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是矩形?
是矩形?
![]() 当
当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形?
是正方形?
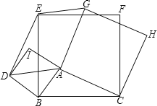
【答案】![]() 四边形
四边形![]() 是平行四边形,理由见解析;
是平行四边形,理由见解析;![]() 当
当![]() 时,平行四边形
时,平行四边形![]() 是矩形;
是矩形;![]() 当
当![]() 且
且![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
【解析】
(1)根据全等三角形的判定定理SAS证得△BDE≌△BAC,所以全等三角形的对应边DE=AG.然后利用正方形对角线的性质、周角的定义推知∠EDA+∠DAG=180°,易证ED∥GA;最后由“一组对边平行且相等”的判定定理证得结论;
(2)根据“矩形的内角都是直角”易证∠DAG=90°.然后由周角的定义求得∠BAC=135°;
(3)由“正方形的内角都是直角,四条边都相等”易证∠DAG=90°,且AG=AD.由□ABDI和□ACHG的性质证得,AC=![]() AB.
AB.
![]() 图中四边形
图中四边形![]() 是平行四边形.理由如下:
是平行四边形.理由如下:
∵四边形![]() 、四边形
、四边形![]() 、四边形
、四边形![]() 都是正方形,
都是正方形,
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴![]() (同为
(同为![]() 的余角).
的余角).
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() 是正方形
是正方形![]() 的对角线,
的对角线,
∴![]() .
.
∵![]() ,
,
![]()
![]()
![]()
∴![]()
∴![]() ,
,
∴四边形![]() 是平行四边形(一组对边平行且相等).
是平行四边形(一组对边平行且相等).

![]() 当四边形
当四边形![]() 是矩形时,
是矩形时,![]() .
.
则![]() ,
,
即当![]() 时,平行四边形
时,平行四边形![]() 是矩形;
是矩形;
![]() 当四边形
当四边形![]() 是正方形时,
是正方形时,![]() ,且
,且![]() .
.
由![]() 知,当
知,当![]() 时,
时,![]() .
.
∵四边形![]() 是正方形,
是正方形,
∴![]() .
.
又∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∴![]() .
.
∴当![]() 且
且![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.

练习册系列答案
相关题目