题目内容
【题目】已知二次函数y=ax2+bx+c的图象与x轴交于点(﹣2,0)、(x1,0),且1<x1<2,与y轴正半轴的交点在(0,2)的下方,在原点的上方.下列结论:①4a﹣2b+c=0;②2a﹣b<0;③2a﹣b>﹣1;④2a+c<0;⑤b>a;其中正确结论的个数是( )
A. 2 B. 3 C. 4 D. 5
【答案】C
【解析】
把x=-2代入y=ax2+bx+c得:y=4a-2b+c=0即可判断①;求出a b c的符号,根据两个根之和为负且-![]() >-1,即可判断⑤,根据4a-2b+c=0和a+b+c>0即可判断④,根据-1<-
>-1,即可判断⑤,根据4a-2b+c=0和a+b+c>0即可判断④,根据-1<-![]() <0,求出后即可判断②,根据4a-2b+c=0推出2a-b=-
<0,求出后即可判断②,根据4a-2b+c=0推出2a-b=-![]() c,根据二次函数与y轴的交点位置即可判断③.
c,根据二次函数与y轴的交点位置即可判断③.
∵二次函数的图象与x轴交于点(2,0)、(x1,0),且1<x1<2,
∴把x=2代入y=ax2+bx+c得:y=4a2b+c=0,∴①正确;
∵二次函数的图象开口向下,
∴a<0,
∵二次函数的图象与x轴交于点(2,0)、(x1,0),且1<x1<2,
∴两根之积为负,![]() <0,即c>0,
<0,即c>0,
![]() <0,即a、b同号,b<0,
<0,即a、b同号,b<0,
两个根之和为负且![]() >1,即a<b<0,∴⑤正确;
>1,即a<b<0,∴⑤正确;
∵把(2,0)代入y=ax2+bx+c得:4a2b+c=0,
∴即2b=4a+c<0(因为b<0),
∵当x=1时,a+b+c>0,
∴2a+2b+2c>0,
∴6a+3c>0,
即2a+c>0,∴④错误;
∵二次函数的图象与x轴交于点(2,0)、(x1,0),且1<x1<2,
∴1<![]() <0,
<0,
∵a<0,
∴2a>b,
∴0>2ab,
即2ab<0,∴②正确;
∵把x=2代入y=ax2+bx+c得:y=4a2b+c=0,
4a2b=c,
2ab=![]() c,
c,
∵O<c<2,
∴2ab>1,∴③正确;
正确的有4个。
故选C.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案【题目】观察下表:
x | 2.1 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 |
y=x2﹣2x﹣2 | ﹣1.79 | ﹣1.56 | ﹣1.31 | ﹣1.04 | ﹣0.75 | ﹣0.44 | ﹣0.11 | 0.24 | 0.61 |
则一元二次方程x2﹣2x﹣2=0在精确到0.1时一个近似根是 ________ ,利用抛物线的对称性,可推知该方程的另一个近似根是________ .
【题目】为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
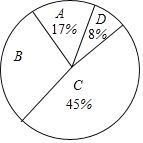
请根据所给信息,解答以下问题:
(1)表中a=___,b=___;
(2)请计算扇形统计图中B组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率。