题目内容
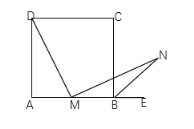
【题目】在平面直角坐标中,边长为2的正方形![]() 的两顶点
的两顶点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在原点.现将正方形
在原点.现将正方形![]() 绕
绕![]() 点顺时针旋转,当
点顺时针旋转,当![]() 点第一次落在直线
点第一次落在直线![]() 上时停止旋转,旋转过程中,
上时停止旋转,旋转过程中,![]() 边交直线
边交直线![]() 于点
于点![]() ,
,![]() 边交
边交![]() 轴于点
轴于点![]()

(1)求边![]() 在旋转过程中所扫过的面积;
在旋转过程中所扫过的面积;
(2)旋转过程中,当![]() 和
和![]() 平行时,求正方形
平行时,求正方形![]() 旋转的度数;
旋转的度数;
(3)设![]() 的周长为
的周长为![]() ,在旋转正方形
,在旋转正方形![]() 的过程中,
的过程中,![]() 值是否有变化?请证明你的结论.
值是否有变化?请证明你的结论.
【答案】(1)π/2(2)22.5°(3)周长不会变化,证明见解析
【解析】
(1)面积=OA![]() OA
OA![]() π
π![]() 45/360=π/2
45/360=π/2
(2)当MN和AC平行时,AM/AB=CN/CB
因AB=CB,故AM=CN,△OAM≌△OCN
∠AOM=∠CON
又∠CON=∠YOA(因同时旋转),∠CON+∠YOA=45°,故∠YOA=22.5°
(3)周长不会变化。
延长MA交Y轴于D点,则可证:
△OAD≌△OCN, AD=CN,OD=ON
△OMD≌△OMN,MN=MD=MA+AD=MA+NC
所以△MBN的周长为P=BM+BN+MN=BM+BN+MA+NC=AB+BC=2+2=4
(1))因为A点第一次落在直线y=x上时停止旋转,所以OA旋转了45度.所以OA在旋转过程中所扫过的面积为π/2
(2)当MN和AC平行时,∠AOM=∠CON,因同时旋转,∠CON=∠YOA,即正方形![]() 旋转的度数为22.5°
旋转的度数为22.5°
(3) 延长MA交Y轴于D点,证得△OAD≌△OCN,△OMD≌△OMN,据此即可证明△MNP的周长等于正方形边长的2倍,据此即可求解

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目