题目内容
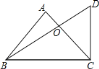
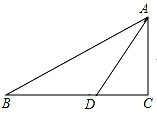
【题目】已知,如图,∠C=90°,∠B=30°,AD是△ABC的角平分线.
(1)求证:BD=2CD;
(2)若CD=2,求△ABD的面积.
【答案】(1)见解析;(2)6![]()
【解析】
(1)过D作DE⊥AB于E,依据角平分线的性质,即可得到DE=CD,再根据含30°角的直角三角形的性质,即可得出结论;
(2)依据AD=BD=2CD=4,即可得到Rt△ACD中,![]() ,再根据△ABD的面积=
,再根据△ABD的面积=![]() 进行计算即可.
进行计算即可.
解:(1)如图,过D作DE⊥AB于E,
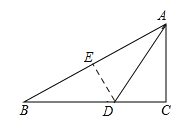
∵∠C=90°,AD是△ABC的角平分线,
∴DE=CD,
又∵∠B=30°,
∴Rt△BDE中,DE=![]() BD,
BD,
∴BD=2DE=2CD;
(2)∵∠C=90°,∠B=30°,AD是△ABC的角平分线,
∴∠BAD=∠B=30°,
∴AD=BD=2CD=4,
∴Rt△ACD中,AC=![]() ,
,
∴△ABD的面积为![]() .
.

练习册系列答案
相关题目
【题目】某中学七、八年级各选![]() 名同学参加“创全国文明城市”知识竞赛,计分
名同学参加“创全国文明城市”知识竞赛,计分![]() 分制,选手得分均为整数,成绩达到
分制,选手得分均为整数,成绩达到![]() 分或
分或![]() 分以上为合格,达到
分以上为合格,达到![]() 分或
分或![]() 分以上为优秀,这次竞赛后,七、八年级两支代表队成绩分布的条形统计图和成绩分析表如下,其中七年级代表队得
分以上为优秀,这次竞赛后,七、八年级两支代表队成绩分布的条形统计图和成绩分析表如下,其中七年级代表队得![]() 分、
分、![]() 分选手人数分别为
分选手人数分别为![]() ,
,![]() .
.
队列 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 |
|
|
|
|
|
八年级 |
|
|
|
|
|
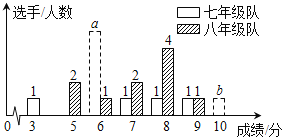
(1)根据图表中的数据,求![]() ,
,![]() 的值.
的值.
(2)直接写出表中的![]() ,
,![]() .
.
(3)你是八年级学生,请你给出两条支持八年级队成绩好的理由.