题目内容
已知关于 的一元二次方程
的一元二次方程 .
.
(1)求证:方程总有两个实数根;
(2)若m为整数,当此方程有两个互不相等的负整数根时,求m的值;
(3)在(2)的条件下,设抛物线 与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP=
与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP= BC,求点P的坐标.
BC,求点P的坐标.
(1)证明见解析;(2)1;(3)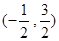 或
或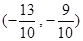 .
.
解析试题分析:(1)证明一元二次方程根的判别式大于等于0即可.
(2)解一元二次方程,根据方程有两个互不相等的负整数根列不等式求解即可.
(3)求出BC的长,由OP= BC求得OP;应用待定系数法求出BC 的解析式,从而由点P在直线BC上,设
BC求得OP;应用待定系数法求出BC 的解析式,从而由点P在直线BC上,设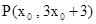 ,应用勾股定理即可求得点P的坐标.
,应用勾股定理即可求得点P的坐标.
(1)∵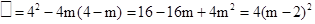 ≥0,
≥0,
∴方程总有两个实数根.
(2)∵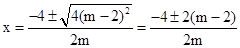 ,
,
∴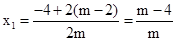 ,
,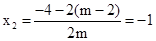 .
.
∵方程有两个互不相等的负整数根,
∴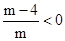 .∴
.∴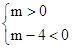 或
或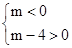 .∴
.∴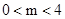 .
.
∵m为整数,∴m=1或2或3.
当m=1时,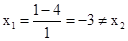 ,符合题意;
,符合题意;
当m=2时,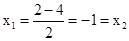 ,不符合题意;
,不符合题意;
当m=3时,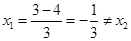 ,但不是整数,不符合题意.
,但不是整数,不符合题意.
∴m=1.
(3)m=1时,抛物线解析式为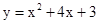 .
.
令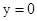 ,得
,得 ;令x=0,得y=3.
;令x=0,得y=3.
∴A(-3,0),B(-1,0),C(0,3).∴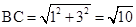 .
.
∴OP= BC
BC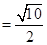 .
.
设直线BC的解析式为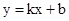 ,
,
∴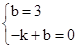 ,∴
,∴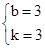 .
.
∴直线BC的解析式为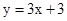 .
.
设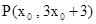 ,由勾股定理有:
,由勾股定理有: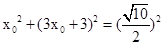 ,
,
整理,得 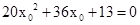 ,解得
,解得 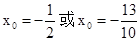 .
.
∴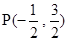 或
或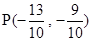 .
.
考点:1.一元二次方程根的判别式;2.解一元二次方程;3.待定系数法的应用;4.曲线上点的坐标与方程的关系;5.勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与x轴,y轴分别相交于点B,点C,经过B、C两点的抛物线
与x轴,y轴分别相交于点B,点C,经过B、C两点的抛物线 与x轴的另一交点为A,顶点为P,且对称轴是直线
与x轴的另一交点为A,顶点为P,且对称轴是直线 .
. ?若存在,请求出点Q的坐标;若不存在,请说明理由.
?若存在,请求出点Q的坐标;若不存在,请说明理由.
 与抛物线
与抛物线 交于A、B两点,
交于A、B两点, 时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
 (x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A. ?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.
?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.

 交坐标轴于A、B、D三点,过点D作
交坐标轴于A、B、D三点,过点D作 轴的平行线交抛物线于点C.直线l过点E(0,-
轴的平行线交抛物线于点C.直线l过点E(0,-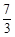 ),且平分梯形ABCD面积.
),且平分梯形ABCD面积.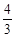 ,求点P的坐标.
,求点P的坐标.
 .等腰直角△EFG中,EF=4, ∠EGF=45°,且△EFG与□ABCD位于直线AD的同侧,点F与点D重合,GF与AD在同一直线上.△EFG从点D出发以每秒1个单位的速度沿射线DA方向平移,当点G到点A时停止运动;同时点P也从点A出发,以每秒3个单位的速度沿折线AD→DC方向运动,到达点C时停止运动,设运动的时间为t.
.等腰直角△EFG中,EF=4, ∠EGF=45°,且△EFG与□ABCD位于直线AD的同侧,点F与点D重合,GF与AD在同一直线上.△EFG从点D出发以每秒1个单位的速度沿射线DA方向平移,当点G到点A时停止运动;同时点P也从点A出发,以每秒3个单位的速度沿折线AD→DC方向运动,到达点C时停止运动,设运动的时间为t. 的长度;
的长度; 平移的过程中,记
平移的过程中,记 相互重叠的面积为
相互重叠的面积为 ,请直接写出面积
,请直接写出面积 的函数关系式,并写出
的函数关系式,并写出 与线段
与线段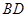 交于点
交于点 ,连接
,连接 .是否存在这样的时间
.是否存在这样的时间 为等腰三角形?若存在,求出对应的
为等腰三角形?若存在,求出对应的

 ),当t =4秒时:
),当t =4秒时:
