题目内容
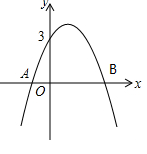
如图1,□ABCD中,对角线BD⊥AB,AB=5,AD边上的高为 .等腰直角△EFG中,EF=4, ∠EGF=45°,且△EFG与□ABCD位于直线AD的同侧,点F与点D重合,GF与AD在同一直线上.△EFG从点D出发以每秒1个单位的速度沿射线DA方向平移,当点G到点A时停止运动;同时点P也从点A出发,以每秒3个单位的速度沿折线AD→DC方向运动,到达点C时停止运动,设运动的时间为t.
.等腰直角△EFG中,EF=4, ∠EGF=45°,且△EFG与□ABCD位于直线AD的同侧,点F与点D重合,GF与AD在同一直线上.△EFG从点D出发以每秒1个单位的速度沿射线DA方向平移,当点G到点A时停止运动;同时点P也从点A出发,以每秒3个单位的速度沿折线AD→DC方向运动,到达点C时停止运动,设运动的时间为t.
(1)求 的长度;
的长度;
(2)在 平移的过程中,记
平移的过程中,记 与
与 相互重叠的面积为
相互重叠的面积为 ,请直接写出面积
,请直接写出面积 与运动时间
与运动时间 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
(3)如图2,在运动的过程中,若线段 与线段
与线段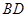 交于点
交于点 ,连接
,连接 .是否存在这样的时间
.是否存在这样的时间 ,使得
,使得 为等腰三角形?若存在,求出对应的
为等腰三角形?若存在,求出对应的 值;若不存在,请说明理由.
值;若不存在,请说明理由.

(1)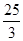 ;(2)
;(2)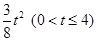 ;
;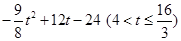 ;
;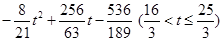 ;
;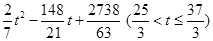 ;(3)
;(3)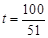 、
、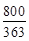 或
或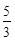 .
.
解析试题分析:(1)过B作BH⊥AD,垂足为H,易证△ABH∽△BDH,求出DH=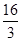 .然后由勾股定理求出AH=3,从而AD的长可求;
.然后由勾股定理求出AH=3,从而AD的长可求;
(2)分四种运动变化进行分类讨论,得出面积s与运动时间t的函数关系式及t的取值范围;
(3)存在.根据等腰三角形的判定,即可求出时间t的值.
(1)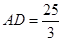
(2)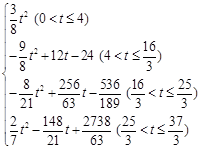
(3) 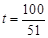 、
、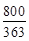 或
或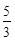 时,△DPQ是等腰三角形.
时,△DPQ是等腰三角形.
考点:1.相似三角形的判定与性质;2.二次函数的解析式.

练习册系列答案
相关题目
 x+m与抛物线y=
x+m与抛物线y= S△NBC,求直线MN的解析式;
S△NBC,求直线MN的解析式;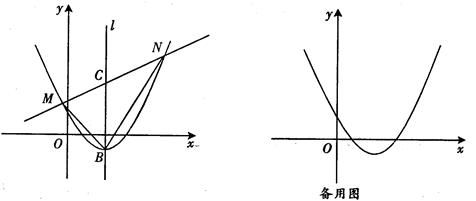
 与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1)。
与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1)。
 的一元二次方程
的一元二次方程 .
. 与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP=
与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP= BC,求点P的坐标.
BC,求点P的坐标. 分别与x轴,y轴交于过点A,B,点C是第一象限内的一点,且AB=AC,AB⊥AC,抛物线
分别与x轴,y轴交于过点A,B,点C是第一象限内的一点,且AB=AC,AB⊥AC,抛物线 经过A,C两点,与
经过A,C两点,与 轴的另一交点为D.
轴的另一交点为D.