题目内容
(11分)如图,已知抛物线y=x2+bx+c经过A(-1,0)、B(4,5)两点,过点B作BC⊥x轴,垂足为C.
(1)求抛物线的解析式;
(2)求tan∠ABO的值;
(3)点M是抛物线上的一个点,直线MN平行于y轴交直线AB于N,如果以M、N、B、C为顶点的四边形是平行四边形,求出点M的横坐标.
(1)抛物线的解析式:y=x2-2x-3;
(2)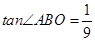 ;
;
(3)点M有4个,其横坐标分别为: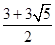 ,
,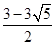 ,
,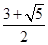 ,
,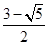 .
.
解析试题分析:(1)将A(-1,0)、B(4,5)分别代入y=x2+bx+c求出b和c的值即可;
(2)过点O作OH⊥AB,垂足为H,根据勾股定理可求出AB的长,进而得到:在Rt△BOH中,tan∠ABO=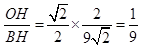 .
.
(3)设点M的坐标为(x,x2-2x-3),点N的坐标为(x,x+1),在分两种情况:当点M在点N的上方时和当点M在点N的下方时,则四边形NMCB是平行四边形讨论求出符合题意的点M的横坐标即可.
(1)将A(-1,0)、B(4,5)分别代入y=x2+bx+c,得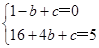 ,
,
解得b=-2,c=-3.
∴抛物线的解析式:y=x2-2x-3.
(2)在Rt△BOC中,OC=4,BC=5.
在Rt△ACB中,AC=AO+OC=1+4=5,
∴AC=BC.
∴∠BAC=45°,AB=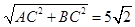 .
.
如图,过点O作OH⊥AB,垂足为H.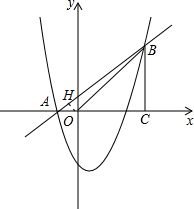
在Rt△AOH中,OA=1,
∴AH=OH=OA×sin45°=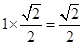 ,
,
∴BH=AB-AH=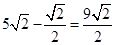 ,
,
在Rt△BOH中,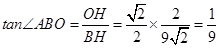 .
.
(3)直线AB的解析式为:y=x+1.
设点M的坐标为(x,x2-2x-3),
点N的坐标为(x,x+1),
①如图,当点M在点N的上方时, 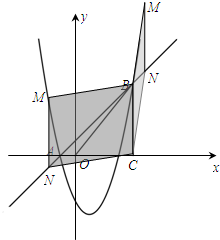
则四边形MNCB是平行四边形,MN=BC=5.
由MN=(x2-2x-3)-(x+1)=x2-2x-3-x-1=x2-3x-4,
解方程x2-3x-4=5,
得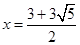 或
或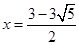 .
.
②如图,当点M在点N的下方时,则四边形NMCB是平行四边形,NM=BC=5.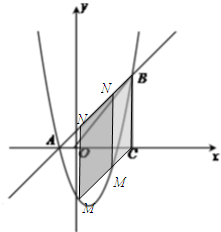
由MN=(x+1)-(x2-2x-3)=x+1-x2+2x+3=-x2+3x+4,
解方程-x2+3x+4=5,
得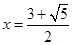 或
或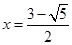 .
.
所以符合题意的点M有4个,其横坐标分别为: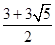 ,
,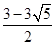 ,
,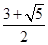 ,
,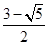 .
.
考点:二次函数综合题.

 与
与 重叠部分面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围;
重叠部分面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围; 是以DG为腰的等腰三角形?若存在,求出t的值;若不存在,说明理由.
是以DG为腰的等腰三角形?若存在,求出t的值;若不存在,说明理由.

 与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1)。
与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1)。

 的一元二次方程
的一元二次方程 .
. 与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP=
与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP= BC,求点P的坐标.
BC,求点P的坐标. 分别与x轴,y轴交于过点A,B,点C是第一象限内的一点,且AB=AC,AB⊥AC,抛物线
分别与x轴,y轴交于过点A,B,点C是第一象限内的一点,且AB=AC,AB⊥AC,抛物线 经过A,C两点,与
经过A,C两点,与 轴的另一交点为D.
轴的另一交点为D.
