Question

在直角坐标系xOy中，已知点P是反比例函数y＝（x＞0）图象上一个动点，以P为圆心的圆始终与y轴相切，设切点为A．
（1）如图1，⊙P运动到与x轴相切，设切点为K，试判断四边形OKPA的形状，并说明理由．
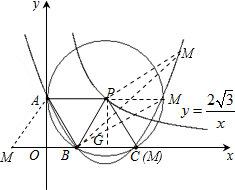
（2）如图2，⊙P运动到与x轴相交，设交点为B，C．当四边形ABCP是菱形时：
①求出点A，B，C的坐标．
②在过A，B，C三点的抛物线上是否存在点M，使△MBP的面积是菱形ABCP面积的？若存在，试求出所有满足条件的M点的坐标；若不存在，试说明理由．

Answer 1

(1) 四边形OKPA是正方形；（2）A（0， ），B（1，0），C（3，0）；（3）；（0，），（3，0），（4，），（7，8）．

解析试题分析：（1）四边形OKPA是正方形．当⊙P分别与两坐标轴相切时，PA⊥y轴，PK⊥x轴，x轴⊥y轴，且PA=PK，可判断结论；
（2）①连接PB，设点P（x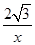，），过点P作PG⊥BC于G，则半径PB=PC，由菱形的性质得PC=BC，可知△PBC为等边三角形，在Rt△PBG中，∠PBG=60°，PB=PA=x，PG=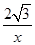，利用sin∠PBG=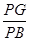，列方程求x即可；
②求直线PB的解析式，利用过A点或C点且平行于PB的直线解析式与抛物线解析式联立，列方程组求满足条件的M点坐标即可．
（1）四边形OKPA是正方形．
证明：∵⊙P分别与两坐标轴相切，
∴PA⊥OA，PK⊥OK．
∴∠PAO=∠OKP=90°．
又∵∠AOK=90°，
∴∠PAO=∠OKP=∠AOK=90°．
∴四边形OKPA是矩形．
又∵AP=KP，
∴四边形OKPA是正方形．
（2）①连接PB，设点P的横坐标为x，则其纵坐标为．

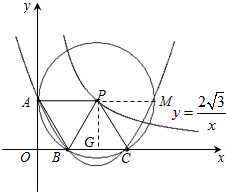
过点P作PG⊥BC于G．
∵四边形ABCP为菱形，
∴BC=PA=PB=PC（半径）．
∴△PBC为等边三角形．
在Rt△PBG中，∠PBG=60°，PB=PA=x，
PG=  sin∠PBG=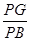，即＝．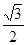
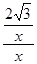解之得：x=±2（负值舍去）．
∴PG=，PA=BC=2．P(2,  )
易知四边形OGPA是矩形，PA=OG=2，BG=CG=1，
∴OB=OG-BG=1，OC=OG+GC=3．
∴A（0， ），B（1，0），C（3，0）．
②设二次函数解析式为：y=ax²+bx+c．
据题意得：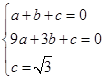
解之得：．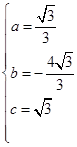
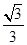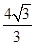∴二次函数关系式为：y＝x²?x+

设直线BP的解析式为：y=ux+v，据题意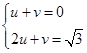得：解之得：．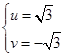
∴直线BP的解析式为：y= x-，
过点A作直线AM∥BP，则可得直线AM的解析式为：y＝x+．
解方程组：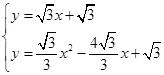
得：；．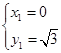
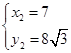过点C作直线CM∥PB，则可设直线CM的解析式为：y＝x+t．
∴0=3+t．
∴t＝?3．
∴直线CM的解析式为：y＝x?3．
解方程组：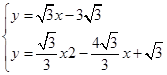
得：；．．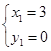
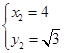综上可知，满足条件的M的坐标有四个，分别为：（0，），（3，0），（4，），（7，8）．
考点: 二次函数综合题．