题目内容
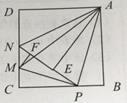
【题目】如图所示,△ABC是等边三角形,D、E分别是BC、AC上一点,且AE=CD,AD,AD、BE交于P,过B作BQ⊥AD于Q,若QP=3cm,PE=1cm,求AD的长。

【答案】7cm
【解析】
根据题意通过“边角边”证明△BAE≌△ACD,得到BE=AD,∠DAC=∠EBA,根据三角形外角的性质求得∠BPQ=60°,然后在Rt△BQP中,求得BP的长,则根据AD=BE=BP+PE即可得到答案.
解:∵△ABC是等边三角形,
∴∠BAC=∠C=60°,AB=AC,
又∵AE=CD,
∴△BAE≌△ACD(SAS),
∴BE=AD,∠DAC=∠EBA,
∴∠BPQ=∠EBA+∠BAP=∠DAC +∠BAP=60°,
又∵BQ⊥AD,
∴∠BQP=90°,
∴∠QBP=30°,
∴QP=![]() BP,
BP,
∵QP=3,
∴BP=6,
∵PE=1,
∴AD=BE=BP+PE=6+1=7.
答:AD的长为7cm.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目